Introduction
The present report aims at testing the current highway mileage of low-mileage fleet minivans of one of the automobile producers. Recently, the car manufacturer received several complaints about the highway mileage of their latest model minivan. The customers claim that the car makes less than the advertised 28 miles per gallon. The present report aims at testing if the complaints are true. For this purpose, a sample of 35 randomly-selected low-mileage fleet minivans of the latest model were elected, and their highway mileage per gallon was measured. Statistical analysis is used to understand if the actual mileage of the cars is below the advertised value.
Sample Mean, Standard Deviation, and Confidence Interval
Calculating the Confidence Interval
First, the confidence interval for the mean mileage per gallon of the minivans was calculated. In order to calculate the confidence interval, the sample size, the sample mean statistic, standard deviation, and the z value for the alpha are needed (McClaive, et al., 2018). The calculations conducted in Excel demonstrated that the sample mean was 26.72, the sample size was 2.10, the sample size was 35 minivans, and the z-value of 1.96 (for alpha of 0.05) was used).
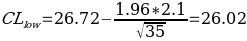
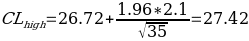
Interpreting the Confidence Interval
The calculations demonstrated that the 95% confidence interval for the population mean was [26.02; 27.42). In other words, the mean highway mileage of the low-mileage fleet minivans lies between 26.02 and 27.42 miles per gallon with 95% certainty. The advertised mileage per gallon is 28, which is above the 95% confidence interval of the calculated population mean. This value was calculated using a sample of 35 randomly selected minivans.
The fact that the advertised mileage of the latest model of minivans is above the higher bound of the 95% confidence interval may be a sign of worry for the company. The confidence interval demonstrated that there is a high chance that the actual mileage per gallon of the new fleet lies above the actual mean mileage per gallon. Even though there is still a small chance that there is no problem with the current mileage per gallon of the new cars (McClaive, et al., 2018). However, that chance is only 5%.
Hypothesis Testing: Two-Tail Test and One-Tail Test
Calculating a Two-Tail Test
A two-tailed one-sample t-test was run to understand if the population mean differed significantly from the hypothesized value of 28. The null and the alternative hypotheses for the t-test are provided below:
- H0: The population mean of the mileage per gallon of the new minivans is 28.
- HA: The population mean of the mileage per gallon of the new minivans is significantly different from 28.
The results of the t-test demonstrated that the mean mileage per gallon of the new minivans (M = 26.72, SD = 2.1) was significantly different from 28 with a 95% certainty (t(34) = -3.61, p = 0.001). The t-test was conducted using excel and is submitted separately from the present report.
Interpreting the Two-Tail Test
The p-value (p = 0.001) was below the alpha level of 0.05, and the t-statistic (t(34) = -3.61) was below the critical value (-2.03) of the two-tailed test, the null hypothesis was rejected, and the alternative hypothesis was accepted (Carlson & Winquist, 2017). In other words, the test demonstrated that the population mean of the mileage per gallon of the new minivans is significantly different from the advertised value of 28 miles per gallon with a 95% certainty. This implies that the complaints of customers were not due to a chance, and the company needs to address the problem of the difference between the actual mileage per gallon and the advertised mileage per gallon.
Calculating a One-Tail Test
A one-tailed one-sample t-test was conducted to understand if the population mean mileage per gallon was significantly below the advertised value of 28. The null and alternative hypotheses for this test are provided below:
- H0: The population mean of the mileage per gallon of the new minivans is 28.
- HA: The population mean of the mileage per gallon of the new minivans is significantly below 28.
The results revealed that the mean mileage per gallon of the new minivans (M = 26.72, SD = 2.1) was significantly different from 28 with a 95% certainty (t(34) = -3.61, p < 0.001). The t-test was conducted using excel and is submitted separately from the present report.
Interpreting the One-Tail Test
The p-value (p = 0.001) was below the alpha level of 0.05, and the t-statistic (t(34) = -3.61) was below the critical value (-1.69) of the one-tailed test, the null hypothesis was rejected, and the alternative hypothesis was accepted (Carlson & Winquist, 2017). In other words, the test demonstrated that the population mean of the mileage per gallon of the new minivans is significantly below the advertised value of 28 miles per gallon with a 95% certainty. This implies that the complaints of customers were not due to a chance, and the company needs to address the problem of the difference between the actual mileage per gallon and the advertised mileage per gallon.
Conclusions
Methods
The results of the analysis revealed that the mean mileage per gallon in the new low-mileage minivan fleet is lower than the advertised mileage of 28 miles per gallon with at least a 95% certainty. The analysis of p-values revealed that the possibility of the mileage being different from 28 miles per gallon is 99.999%, according to the two-tailed one-sample t-test. The certainty was even higher for the one-tailed one-sample t-test (>99.999%), which implies that the possibility that the actual mean mileage of the new fleet was lower than 28 miles per gallon. Thus, it may be concluded that the one-tailed one-sample t-test provided higher certainty for addressing the problem.
According to Moore and Notz (2021), one-tailed t-tests are conducted when the researcher needs to understand if there is a difference between the population mean value and the hypothesized mean value in one direction. Since the present research aimed at understanding if the actual mileage per gallon of the new minivan fleet was lower than the advertised value of 28 miles per gallon, it was more appropriate to use a one-tailed test. Since this test provided even more certainty than the two-tailed test, it may be concluded that the actual mileage per hour was lower than that claimed by the manufacturer.
The Manufacturer’s Claim
The result of the analysis revealed that the manufacturer’s claim concerning the mileage per gallon of the new minivan fleet was wrong with a high degree of certainty. In particular, there is more than 99.99% possibility that the mean mileage per gallon of the new minivans is below 28 miles per gallon. This implies that the complaints filed by the customers are explained not by chance but by the fact that the mileage per gallon of the new cars was lower than the advertised value.
Summary
Three statistical tests were conducted to test the hypothesis that the mean value of highway mileage per hour of the new minivan fleet was below 28 miles per gallon. The calculation of 95% confidence interval revealed that the advertised mileage per gallon was above the higher bound of the confidence interval. A two-tailed one-sample t-test revealed that there was 99.999% possibility that the actual mileage per gallon was different from the advertised value, while a one-tailed one-sample t-test demonstrated that there was >99.999% possibility that the actual mileage per gallon of the new fleet was below the advertised value.
Recommendations
Since currently the company misinforms its customers about the mileage per hour of the new fleet, it is recommended to change the advertised value to 27 miles per gallon, as it was demonstrated that this value lies within the 95% confidence interval. Additionally, the company needs to inform its current customers about the findings of the present research to make amends to them to ensure customer loyalty in the future. A formal investigation is also needed to determine the reason for the discrepancies between the actual mileage per gallon and the advertised mileage per gallon.
References
Carlson, K. A., & Winquist, J. R. (2017). An introduction to statistics: An active learning approach (2nd ed.). Thousand Oaks, CA: Sage.
McClaive, J., Benson, G., & Sincich. (2018). Statistics for business and economics. Pearson.
Moore, D., & Notz., W. (2021). The Basic Practice of Statistics. Macmillan Learning.