The word implies a set of interconnected events and phenomena. It means that nothing emerges, develops, and disappears without introducing some changes to an external environment. That is why it is possible to mention that the world consists of dynamic systems, and it is necessary to find appropriate tools and methods to understand them. The importance to identify and measure a relationship between various objects increases when it comes to the use of the mechanical system. One can say that a frequency response function (FRF) is a suitable option in this case.
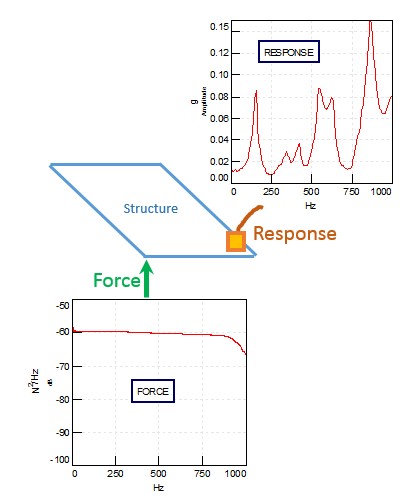
An FRF is useful when it is necessary to identify a correlation between input and output data. According to the Eomys, it is “a function used to quantify the response of a system to an excitation, normalized by the magnitude of this excitation, in the frequency domain” (par. 1). In other words, one can use this function to determine how changes in the input force can affect the output data. For example, Figure 1 by Siemens demonstrates that there is an evident connection between the input force (below) and the output one (above). It is necessary to emphasize that a stimulus results in proportional responses in the graph.
Maxwell’s Reciprocity Theorem is suitable to explain the principles of the FRF. The given theorem focuses on distinct points on a linear structure, and Maxwell identified the symmetric flexibility matrix of linear systems. If, for example, object A creates a force that leads to the displacement of object B, this displacement will be identical to the one that objects A experiences because of the force created by object B. It is possible to verify the given theorem with the help of simple experiments, and the one with an impact hammer and an accelerometer are among them.
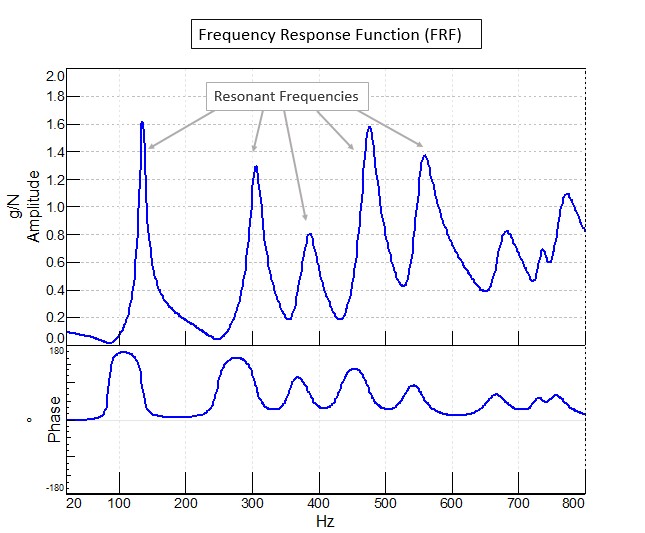
It is possible to use the FRF in many areas of knowledge, including mechanical, acoustical, combined mechanical and acoustical, as well as rotational mechanical systems. In each of them, the FRF can help determine what changes will occur because of the input influence. The possible variants refer to acceleration, displacement, velocity, sound pressure, rotational displacement, and others. When it comes to analyzing the frequency of stable structures, it is a typical case that they can experience the force with a flat frequency response. Figure 2 by Siemens demonstrates that the flat input force usually unveils the natural frequencies of the structure under test. Thus, even a slight deviation in this force can result in noticeable resonant frequencies of the object. It denotes that the structure under test reveals its resonant frequencies, and the presence of evident peaks in the graph below justifies this idea.
There is no doubt that the FRF is a significant measurement tool in the sphere of science. It is so because it helps predict how an object will respond to a particular input force. For example, architects use the given function to identify how rigid or stable their buildings are regarding natural disasters or other harmful events. These data help achieve the highest safety standards throughout the world. In addition to that, the FRF is useful since it allows determining what level of the sound pressure will emerge following a particular volume acceleration. These details are significant because they lead to the creation of appropriate sound equipment that will meet the required standards and will not become disabled because of a slight increase in volume acceleration.
Works Cited
Eomys. “What Is a FRF (Frequency Response Function)?” 2020. Web.
Siemens. “What Is Frequency Response Function (FRF)?” 2020, Web.