Introduction
The concept of future and present value lies at the center of finance. Businesses strive to perform something worth resulting in a future payout. Therefore, it is recommendable to calculate their future outflow or inflow value using the present value. This calculation heavily relies on the time value of money, which is crucial to understand the concept enabling managers and business owners to balance their financial accounts. In this case, George Washington birthday will be chosen, and the date data will be used to perform the present and future value calculations.
Significance of George Washington Birthday
George Washington was the founding president of the United States of America. He led the Continental Army to their victory in the revolutionary war, after which he became the first president of the country and ruled for two terms. Furthermore, he came from the middle class in the Northern part of the U.S. and overcame the challenges to become one of the elites in the country. His birthday; 22nd of February 1732, is significant since he did not only shape the ability to adhere to the term limit period in the United States of America presidency, but also believed in democracy (Duling, 2017). His loyalty to the people and law throughout serving for a limit of two terms only has been instrumental since all his successors have emulated him and followed his legislation.
Variable Identification
The calculation of the present and future value will require the discount rate or the annual simple interest, the period of time, the initial deposited amount or the total amount to be received at the end of the period of time. Therefore, the identified components will be vital in the calculation of the future and present value. The applicable formula for this case will be: P. V = F. V/(1 + r)t
Where:
- P. V = the presentmoney value
- F. V = the future money value
- t = the number of years
- r = the annual rate of interest
Another applicable formula is: A = P (1 + r/n)nt
Where:
- A = the investment sfuture value
- P = the initial principal investment value
- r = the annual rate of interest
- n = the number of the interest is compounded per unit
- t = the period the investment was done
Considering the selected birthday of 22nd of February 1732, the variables will be represented as follows:
The day being 22 will represent the number of years. Therefore, the number of years is, 22 years.
The month being February and is equivalent to 2 will represent the interest rate (annually). Therefore, the annual interest rate will be 2%.
Considering the year which is 1732, will be multiplied by 100 and therefore, represents the value of the dollar. Therefore, the initial value will be $(1732 x 100) = $173,200.
Therefore, the built situation is: $1732,200 invested at 2% for a period of 22 years.
Calculations
When businesses invest their money into a venture, they are certain of a payoff in the future. Similarly, there are instances where the fund may fail to generate interest.
Future Value = Present Value
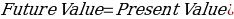
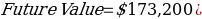
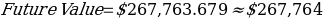
Also, if the investment is compounded monthly, write:
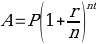
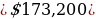
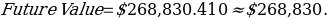
Calculating the balance after t years:
Simple interest earned
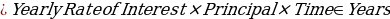
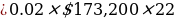
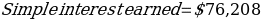
Interest rate of the period
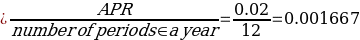
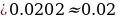
Balance after t years
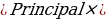
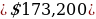
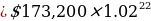
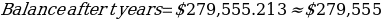
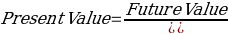
Substituting the values in the equation, I will have:
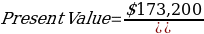
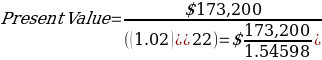
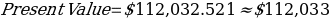
Number of Periods to double
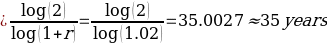
Monthly Payment
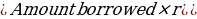
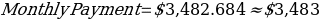
Amount Period
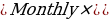
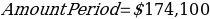
Balance after t deposits
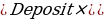
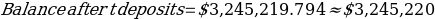
Needed Deposit
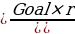
Monthly Annuity Yield
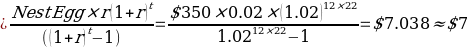
Nest Egg Needed
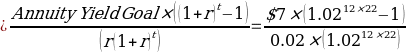
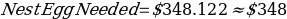
Finance Charge
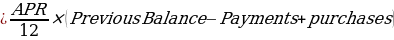
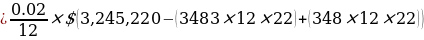
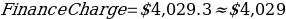
New Balance
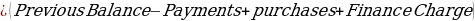
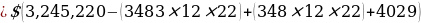

Balance after t minimum Payments
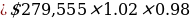
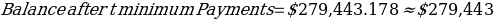
Percent Decrease in Buying Power
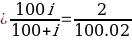
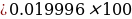
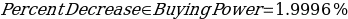
References
Duling, K. (2017). George Washington (1st ed.). Cavendish Square Publishing, LLC.
Shrotriya, V. (2019). Time value of money – the concept and its utility. IJRAR, 6(1), 85-92. Web.