Introduction
This report investigates the amount of thermal energy created in exothermic ionic processes and compares using Hess’s law. This law demonstrates the aspect that enthalpy is a state function. All steps must be performed at the same temperature, and each process’ equations must be balanced (Mark et al., 2018). The Styrofoam cup was utilized as the calorimeter in this research. The heat supplied to the surrounding were neglected in the calculations, and water was concluded to have a heat capacity of 4.184 J/g°C. At standard conditions, namely, at 25º C and 1 atm., the enthalpy change may be calculated as:
- ΔH=q
- ΔH=q= m × C × (ΔT).
Experiments were conducted on the virtual lab website instead of the typical physical lab. The virtual lab offered an alternative way of performing the calorimetry experiments using Hess’s law. The virtual lab saved costs by permitting the performance of the experiments more than once. The temperature change for every process was applied to compute the heat generated in kJ/mol of NaOH. The values x1, x2, and x3 in the equations below indicate the heat values generated during the reactions.
- Experiment I: NaOH(s) → Na+(aq) + OH−(aq) + x1 kJ
- Experiment II: NaOH(s) + HCl(aq) → H2O(l) + Na+(aq) + CL−(aq) + x2 kJ
- Experiment III: NaOH(aq) + HCl(aq) → H2O(l) + Na+(aq) + Cl−(aq) + x3 kJ
The following were the objectives of this experiment:
- Writing a balanced ionic equation for the allocated samples in the experiments.
- To use the calorimetry method, quantify the ΔH values of the three reactions analytically.
- To use these ΔH values in a Hess’s Law calculation to estimate an enthalpy of reaction.
Methods and Materials
The materials and equipment used
Distilled water, solid NaOH, 0.50 M HCl solution, 50-mL graduated cylinders, foam cups, balance, and a thermometer obtained from the stockroom.
Procedure
Click on the virtual Lab to enter the workstation. Clicked ‘File’ then ‘Load an Assignment’ when the lab environment had loaded. Choose ‘Thermochemistry’ from the drop-down menu. Selected ‘Heats of Reaction’ from the drop-down menu. The laboratory was established for the experiment and gathered all needed items at this stage. Placed a 50-mL graduated cylinder and a foam cup on the workstation from the ‘Glassware’ option. Added a balance to the workstation from the ‘Tools’ tab. The distilled water and NaOH pellets were moved to the workstation (Virtual lab, 2022). Fill the foam cup with 50.0 mL distilled water. To do so, pour the water into the graduated cylinder first, then into the foam cup. After moving the water to the graduated cylinder, enter ‘50.0’ and click ‘Pour.’ In the data table, write down the water’s original temperature.
After adding the foam cup, weigh the balance of 1.00 g of NaOH pellets straight into the foam cup. At this point, the balance was removed from the workstation. Fill the foam cup halfway with the liquid of the graduated cylinder and note the maximum temperature and weight of the cup’s contents right away. A temperature probe was used to monitor the highest temperature in the foam cup (Virtual lab, 2022). The second experiment was conducted with 50.0 ml of 0.50 M HCl solution and 1.00g of NaOH pellets. The final experiment was repeated using 25.0 ml of 1.0 M HCl and 25.0 ml of 1.0 M NaOH solutions.
Fill in the value obtained during the trials in the table below with the ‘Data’ section. Experiment 1’s energy, x1, was the energy of the solution for one mole of NaOH pellets. Examined the net ionic equations for experiments 2 and 3 and made a comparable remark about the relevance of x2 and x3 and their relationship to Hess’s law. Calculated the percent difference between the variance.
Results
In the calorimetry investigation, a known weight of reactant is accompanied by a known amount of water. Then the temperature change in the water column is recorded (Archer, 2020). Change in temperature, ΔT = Tfinal – Tinitial, joules (J) are the unit of measuring energy change, and temperatures (T) were measured in degree (°C). The following is a list of corresponding values represented by two significant numbers due to the thermometer probe utilized.
Discussion
The experiment went out without a problem, with no unexpected circumstances that could have caused an inaccuracy. Energy transfer is frequently associated with chemical and physical processes. This experiment was crucial for evaluating three exothermic experiments involving sodium hydroxide and correlating them to Hess’ Law. NaOH pellets dissolved into water in experiment I, and the heat generated by the reaction was known as the heat of NaOH. NaOH pellets reacted with an aqueous HCl in experiment II. As it decomposes in the acid solution, the solid NaOH dissociates into ions before the acid neutralizes it. The heat generated by the reaction was termed the heat of NaOH solution. In experiment III, an aqueous monobasic base (NaOH) reacts with an aqueous monoprotic acid (HCl). The heat of neutralization was the heat generated by the reaction.
Stepwise explanation
Experiment I
Moles = molarity × liters of solution.
Molar mass of NaOH = 40.0g/l
Mass of NaOH used = 1.00g
Moles of NaOH = 1.00g × 1.0mol/40.0g/mol
= 0.025 moles of NaOH
Water used = 50.0ml, density of water = 1.0g/ml, mass = density × volume
=1.0g/ml × 50.0ml
=50.0g of water
C = 4.184 J/g.°C
ΔH=q= -m × C × (ΔT).
= -50.0g × 4.184 J/g.°C × 5.30 °C
ΔHºrxn = -1108.76 J
1KJ = 1000 J
= -1108.76 J × 1KJ/1000 J
qreaction (kJ) = -1.10876 KJ
Net ionic equation: NaOH(aq) → Na+(aq) + OH−(aq)
Experiment II
Molar mass of NaOH = 40.0g/l
Mass of NaOH used = 1.00g
Moles of NaOH = 1.00g × 1.0mol/40.0g/mol
= 0.025 moles of NaOH
HCl used = 50.0ml of 0.50 M HCl, density of HCl = 1.0g/ml
=1.0g/ml × 50.0ml
=50.0g of HCl
C = 4.184 J/g.°C
ΔH=q= -m × C × (ΔT).
= -50.0g × 4.184 J/g.°C × 11.97 °C
ΔHºrxn = -2504.12 J
1KJ = 1000 J
= -2504.12 × 1KJ/1000 J
qreaction (kJ) = -2.50412 KJ
Net ionic equation: OH–(aq) + H+(aq) → H2O(l)
Experiment III
Moles = molarity × liters of solution.
Moles of NaOH = 1.0 M NaOH × 0.025 L
Moles of NaOH = 0.025 moles of NaOH
HCl used = 50.0ml, density of water = 1.0g/ml
=1.0g/ml × 50.0ml
=50.0g of HCl
C = 4.184 J/g.°C
ΔH=q= -m × C × (ΔT).
= -50.0g × 4.184 J/g.°C × 6.67 °C
ΔHºrxn = -1395.36 J
1KJ = 1000 J
= -1395.36 J × 1KJ/1000 J
qreaction (kJ) = -1.39536 KJ
Net ionic equation: OH–(aq) + H+(aq) → H2O(l)
Data analysis
X4 = x1 + x3
= -1.10876 KJ + -1.39536 KJ
= -2.50412 KJ
X5 = X2 – X4
= -2.50412 KJ – -2.50412 KJ
= 0 KJ
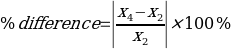
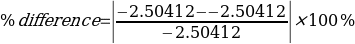
= 0%
The enthalpy changes for x1 and x3 equals the enthalpy change for x2. As a result, the interactions follow the Hess Law.
Conclusion
Finally, the investigation’s objectives were to estimate the enthalpy change of three exothermic processes and connect them to Hess’ Law. Based on the findings, it can be concluded that all of the reactions are exothermic since they generate heat. This is because all of the data from each experiment stage indicate that the temperature rises from its starting point. The percentage error proved the virtual lab could be used to obtain perfect lab results free from mistakes.
References
Archer, W. R., & Schulz, M. D. (2020). Isothermal titration calorimetry: practical approaches and current applications in soft matter. Soft Matter, 16(38), 8760-8774.
Mark, K., Mercier, P., Gonzalez, J., & Yearwood, B. (2018). Thermochemistry: Heat of Neutralization and Hess’s Law [Chemistry].
Virtual lab, thermochemistry (2022). The ChemCollective. Choice Reviews Online, 45(11), 45-6177-45-6177. Web.