Abstract
The aim of this research is to review the origin and subsequent development of calculus over the years through the analysis of two great mathematicians; Isaac Newton of England and Leibniz Gottfried of Germany. It’s clear that calculus served as the quantitative language of science for more than three hundred years and these two were credited with transforming the powerful tool of their thinking into mathematics. We define the four development of calculus as integral, differential, mathematical and modern, and how various methods were invented by geometers influenced the development of calculus. Two properties can be distinguished; derivative and infinitesimal.
We discuss why it’s important to study calculus and identify the main areas of interest.
Greek mathematicians separated algebra and geometry. The Cartesian coordinates and modern symbolism are what gave Isaac Newton and Leibniz Gottfried insights into creating calculus and our focus is how they used the Fundamental Theorem of Calculus into transforming people’s theories into a powerful tool. Although calculus received numerous criticisms at the time of invention, mathematicians succeeded in putting calculus on a firm foundation. To understand their theorem, they clearly understood infinity. Though the applications interplay between discreetness and continuity, these two geometers have described discreet objects by continuous models and use the same applications for solving continuous problems.
Introduction
The subsequent development of calculus is largely due to the ancient geometer’s natural curiosity and their demands of application that provided solutions to mathematical problems. They confronted the problems of finding areas and volumes of various solids- a term referred to as integration; a phrase used throughout the paper. The outstanding work of the previous century’s geometers such as the great Greek Democritus, the works of the Chinese mathematician Liu Hui and Archimedes, to name just a few brought together the techniques of solving calculus problems. Their resembling concepts of derivations and Integration can be recognized in the works of Fermat and Democritus on tangents and finding maxima and minima.
Subsequent Development of Calculus
The mathematics we have today is owed to the great contributors of Indian Mathematicians and astronomers. By 500 AD, Aryabhata had introduced a notion of infinitesimals, based on basic differential calculus to solve integer equations that arose from his astronomical theories. Another Indian classic, Manjula, developed an equation in the 10th century that eventually led to the development of the 12th century Bhaskara II derivative concepts and Rolle’s Theorem (Smith, 2007; Kartz, 1995)).
There would have been no transition between ancient calculus and modern mathematics without the great contributions of the 12th-century Indian geometer Bhaskara II who defined and simplified the derivative and differential coefficient methods along with Rolle’s theorem. Another contribution came from Madhava who brought new perspectives in mathematics that provided a foundation for mathematicians to build their theories on (Connor & Robertson, 2000; Kartz, 1995).
Harappa’s, another Indian mathematician, developed a system of weights and measures and in his analysis discovered that series apart from being decimal in nature, can either be multiplied or divided by 2 and would give main series ratios of 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200 and 500 (Connor & Robertson, 2000). Their contributions collectively discovered scales for measuring length (Indus inch) and inches, an accurate measure for determining the length of the excavated building (Connor & Robertson, 2000).
In the the12th century, a Persian mathematician al Tusi discovered the derivative of cubic polynomials through equations. He devised a formula for finding maxima and minima of curves and derivation function as applied in solving cubic equations which may not have positive solutions. For instance, in order to solve the equation x3 + a = bx, al Tusi finds the maximum point of the curve by using this equation; y= bx- x3.

In the 15th century, the mean value theorem came into existence and was described by another Indian geometer Parameshvara between 1370 to 1460 from the Kerala School of astronomy and mathematics (Connor and Robertson, 2000).
Rolle’s Theorem as discovered by Michel Rolle in 1691 applied a special case of Mean Value Theorem which stated that “if f(x) is a continuous an [a,b] and differentiable on (a,b) and if f(a)=f(b) then there is some c in the interval (a,b) such that f ‘(c) = 0” (Calculus Quest, online). The existence of the special case under the stated hypothesis MVT is because it guarantees the existence of point c with f ‘(c) equals to f(b) – f(a) divided by b-a which then equals to f(b) – f(a) divided by b-a resulting to zero. Rolle’s theorem uses f(x) as a continuous function on the closed interval [a,b] which enables it to achieve the maximum and the minimum points on [a,b]. In a more detailed example, we can see that since f(x) is differentiable on (a,b) and therefore c is an extremum which concludes that f ‘(c) = 0. Or when we are using both the maxima and the minima, he states that f(x) occurs at endpoints. He argues that since f(a)=f(b), the function is never larger or smaller at any of the particular points. In simpler terms, the function f(x) is constant on intervals [a,b] and therefore its derivative is 0 at every point they meet at (a,b) (Bogley, 1996).
In the 17 century, Piere de Fermat invented a trick for evaluating the integral of any power function directly by finding the centers of gravity. He attempted to find solutions to these mathematical problems by applying quadrature variational methods although he could not verify his formula as he failed to extinguish the notion relationship between tangent and summation. His method of tangents is essentially the modern method of finding tangents thereby providing a valuable clue to Newton and Leibniz in their development of the “fundamental development of calculus”. Pierre also invented a technique for finding the centers of gravity of various planes and solid figures hence the influence of quadrature and also provided another way of writing equations (Smith, 2007).
In the 17th century, Isaac Barrow, a European, Pierre de Fermat, Blaise Pascal, John Wallis all discussed the idea of derivatives. In that era, Fermat independently discovered methods for determining maxima, minima, and tangents of various curves, a step that inspired Isaac’s early ideas of developing calculus by drawing tangents (Connor and Robertson, 2000).
Simultaneously, another Japanese mathematician, Kowa Seki around the same period made significant contributions in developing calculus by inventing a method of determining areas of figures using integral and then progressed to the exhaustion method. Geometers’ methods of finding solutions to mathematical problems became obsolete when Newton and Gottfried brought their sophisticated knowledge of mathematics when they developed the fundamental theorem. From these explanations, it’s clear that geometers did not think together in forming whole methods of analysis (Smith, 2007).
Integral Calculus
Democritus, an Egyptian back in Moscow papyrus invented a formula for calculating volumes and areas of the pyramidal frustum in the year1820 B.C. At about the same time, another Greek geometer investigated solutions for finding tangents for curves and solid figures. This method has been shown by expression and investigations to be useful in finding volumes of objects of various curves and fixed axis. Integral calculus can be divided into two categories; definite and indefinite calculus. Integral calculus was developed when geometers were experiencing problems measuring the area of a plane bounded by curved lines. The formula employed function f(x), which is continuous and positive in an interval, and two values a and b(a<b) in the same interval. The function here is the area expressed by a curve while the area of the region is bounded above the curve by straight lines as x=a and x=b and below by the position of the x-axis and points a and b as expressed in (fig 1) (Chapter II, online).
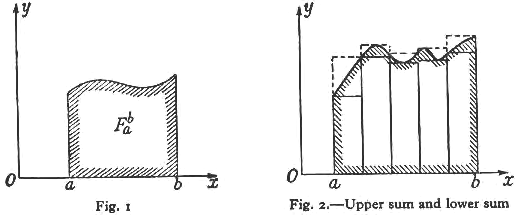
When speaking of an area of a region, we often give assumptions of intuition which is stated in the hypothesis. This area is termed as Fab the definite integral of the function f(x) between the limits a and b. This formula made it possible to measure the areas of curved boundaries by measuring polygons with straight lines by dividing them into recognizable rectangles and triangles. We then realize that subdivision of areas is impossible since it limits the value of a sum of areas of rectangles. If the area of a rectangle is subdivided at the x-axis point between a and b into n equal parts, it will be impossible to determine the areas of such strips than it would have of original surfaces (Chapter II, online).
Figure 2 demonstrates that in order to determine the greatest and least of the function f(x) in each sub-interval, we should replace the corresponding strip by; (1) diving the heights of rectangles into equal parts of the least value of the function and second; by diving the heights of rectangles into the equal greatest value of the function, which gives us two figures illustrated in fig 2. The first figure is drawn by a solid line which has an area that is almost equal to the area Fab while the second is drawn by a broken line which is at least larger as Fab .

Democritus earned the first position in recording the division of objects into an infinite number of cross-sections though he could not rationalize discreet cross-sections with a cone’s smooth slope which was a major obstacle for his continued research. Yet another Greek geometer, Zeno of Elea made significant in-roads in calculus when furthered the infinitesimals formula by articulating the paradoxes they create (Aslaksen, 2006).
Differential Calculus
Differential calculus is a mathematical formula first discovered by Archimedes to find tangents of a curve. He separated points of spirals motions into two components and added them together to arrive at a solution for solving the tangent of a curve. His discoveries concerning volumes and surfaces of solids. The problem at the time was to define the ratios of circumferences of the diameter of a circle and he approached this question by diligently establishing that the upper and the lower bounds of the area of a circle can be made to bound by converging them close to each other (Math pages, online).
Antiphon and Eudoxus presentations and discussions inspired a new method of finding volumes of objects and spheres known as exhaustion. This method was used in calculating areas and volumes of regions and solids by breaking the objects into infinite numbers. Archimedes furthered this method by inventing a heuristic method for finding the volume of spheres and cylinders. He introduced the pi ratio of circumferences and diameters of circles (Math pages, online
Finding a formula for determining the area of a circle was often considered a mathematical challenge before Archimedes’ invention of using a rational number pi in determining the circumference of a circle. In solving this problem, Archimedes divided the circumference of a circle by the diameter. The diagram below shows how he determined the square of a circle by inscribing a polygon.
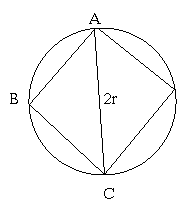
Here the diagonal lines inscribed are the same as the diameter of the circle which has the length 2r and since the squares AB, BC are equal, the length is therefore √2r. He gives the area of the triangle ABC to be A=√2r√2r=2r², a formula that marked the start of approximation of the area of a circle (How Archimedes found the Area of a circle, online).
Archimedes’ second formula of approximating the area of a circle involved hexagon. He divided the hexagon into six triangles as below;
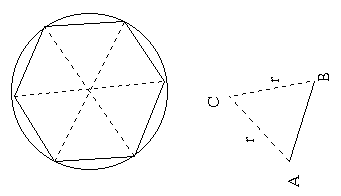
When the triangles are measured separately, the angles would measure 60 degrees, which is one-sixth of the sum of all the angles (360). This proved that the triangles of the hexagon are equilateral. Since the lengths of the sides are r, the height of each triangle would be √3r/2 and therefore the area of the hexagon would be;
A= 6(½rh) =6(½r √3r/2)= 3√3r/2=2.59r²
This formula moved a step closer to the true area of a circle (How Archimedes found the Area of a circle, online).
The third step of Archimedes formula included an n-sided polygon which increased the number of sides (n) in the polygon deriving to the formula of; A=n(Area triangle=n(½ h b). H B for this instance represents the base and the heights of the triangle as shown below;
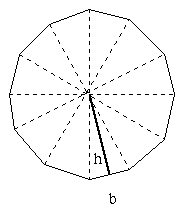
And when the sides of the polygon increases we derive the following formula; A= n (½ h b) = ½ h (n b). nb represents the perimeter of the polygon and when the number of polygons increases, they become closer to the circumference of the circle, and when the height of the triangle (h) increases, the closer they get to the radius of the circle. By approximating the circle by using polygon with more sides, (the greater the number the thinner the triangles), Archimedes got closer to finding the area of the circumference of the circle with the following formula;
A= ½ h (n b) ≈ ½r (2pi r) =pi r²
This formula has developed into modern calculus since the area involves a special constant pi in calculating the circumference to the diameter of the circle; a method that is commonly used today (How Archimedes found the Area of a circle, online).
Modern Calculus
James Gregory invented the second version of the fundamental theorem of calculus in the mid 17 century and later Newton and Leibniz stepped up the ladder by the late 17th century in inventing the modern calculus commonly known as the fundamental theorem of calculus. The two mathematicians took different directions in their research; for example, Gottfried developed mathematical notations and concepts while Newton compiled all the mathematical fields of earlier geometers into one consistent subject and also provided the first applications of calculus. Even though the fundamental of calculus hailed the first published statement is what is now termed as the fundamental theorem of calculus, historians have greatly ignored this fact which made great Geometes like Gregory not to further their discoveries ideas of calculus (Leahy, 2005, p.10)
Newton and Leibniz
Before Newton and Leibniz, calculus was just a general term used in any body of mathematics. Before they came into play, infinitely small numbers were never considered in mathematics. Their insights brought more important meaning in the field of mathematics when they came up with various methods for solving problems related to today’s mathematics. This two used simpler mathematical terms in an attempt to make us understand calculus as they did. In the middle of the 17th century, European mathematics changed from the primary repository of knowledge to Hellenistic mathematics which started the point for research and Europe had become the home for modern thinkers; a mathematics community, and with the advent of enhanced institutions brought new levels of academic integration. We can see that the community lacked formalism and their focus primarily consisted of a disordered mass of various methods, notations, theorem, techniques, and paradoxes which could not be understood (Leahy, 2005, p.10).
Newton’s passion for mathematics started at an early age. He began by investigating physics and geometry then later moved to calculus. His methods were built on a sound foundation using ideas from past geometers like the Greeks and Indians. He introduced his own theory of infinitely small numbers (infinitesimals) to provide solutions to derivatives or slopes. Calculus was part of his scientific inventions of motions and magnitudes. Gottfried’s focus shifted on tangent problems since he believed calculus was a metaphysical explanation of change he planned to look into in the future. His central focus was to formalize the inverse properties between the integral and the differential; this was the first calculus system in which new rhetoric and descriptive terms were created. Their ability to synthesize the insights around them into a universal algorithmic process enabled them to form a new mathematical system that influenced the direction of modern mathematics (Leahy, 2005, p.10).
Newton’s many mathematical discoveries established a transition between ancient calculus and modern mathematics. His incredible aptitude was recognized by many geometers all over the world. At an early age, he quickly learned about the current theories and by 1664, he had already advanced the binomial theorem formula which included fractions and negative exponents, and extended this by applying algebra of finite quantities in an analysis of infinite series. His approach demonstrated how he viewed infinite series as alternative forms (Smith, 2007).
Newton’s development in mathematics began during 1665-1666 during this period which he induced the isolation of Fluxionary calculus-indefinitely small triangle whose area is a function of x and y. He then progressed to reasoning that infinitesimal increases in the abscissa will create a new formula where x=x+O (letter O not a digit 0). He then progressed to calculating the area using the binomial theorem by removing all quantities with the letter O and forming an algebraic expression of the area. His formula created a solution of an area under a curve by considering a momentary increase at a central point at this effect; a formula he called fundamental calculus. In his development admitted to the errors that evolved in mathematics and referred to them as continual flowing motion. He considered variable magnitudes to be generated by motion and not by infinitesimal elements (Smith, 2007).
Newton gave calculus a more rigorous approach when he complied the Methodus fluxional et Serierum Infinitum into definite terms in 1671. This new method shaped and defined how fluxional calculus could be approached. This method used a methodological tool in calculating fluxional calculus in explaining the physical world other than the existing instantaneous motion. His revised calculus became continuity like the continual flowing calculus. The Methodus Fluxionum defined the quantity generated (fluent). For instance, if x and y are fluents, then x and y are the representative fluxions. His inventions continued to develop gradually and were termed in 1676 as “De Quadratura Curvarum”. This method defined the present-day derivative as the ultimate ratios of change which defined the ratio between evanescent increments. He explained the ultimate ratio by appealing to motion-ratio as the increments vanish into nothingness (Smith, 2007).
In Newton’s days, a variable was termed as a fluent that flows with time, and its derivative or rate of change changes with time later termed as “fluxion”. It should be noted that his solid foundation in mathematics helped influence the direction of derivation which could otherwise be ignored. His recognition in magnitudes brought major changes to the current mathematics as he had extensive literature and pursued his own line of analysis. His discovery of binomial theorem, a tool that employed infinitesimals in finding areas under curves and slopes of curves brought major development to calculus (Smith, 2007).
Leibniz
Leibniz defined tangents to be the ratio between ordinates and abscissas and argued that integrals were the sum of the ordinates for infinitesimal intervals in the abscissa. In simple terms, the tangent was the sum of an infinite number of rectangles. He then developed the potential of forming a whole new system of mathematics. Gottfried concentrated on the use of infinitesimals which Newton shied away from in developing his notations and calculus (Mates, 1986, p.158).
In 1675, Gottfried laid the foundation of both integral and differential calculus in experiments that took various forms of notations and used his logical symbolism. With his discovery, he considered time and space as substances and later denoted the infinitesimals differences between abscissas and ordinates as dx and day, and the summation of infinitely many infinitesimally thin rectangles as along as (∫), which become the present integral symbol ∫. His development of notions concepts explained that motioned contained an element of imaginary which limited the basic laws of motion from being discovered. Leibniz notations are used by modern mathematics though the logical base is different from our current one and defined his infinitesimals as relative zeros- which is an evanescent quantity which retains the character of that which is disappearing but instead defines them as “less than any given quantity”. To him, the world was an aggregate of infinitesimal points and lacked the scientific proof for their existence and intended to prove otherwise. The principle of continuity to him and then the validity of calculus were assured. Abraham Robinson, three hundred years after Leibniz showed that using infinitesimals quantities in calculus could be given a solid foundation (Mates, 1986, p.158).
Leibniz’s analytical interpretation of the integral definition considered definite integrals as a number given by an area. He dismissed the idea of intuition and provides his formula by limiting the value by calculating the definition of the integral and the area by providing symbols for calculating integrals. He provides the function f(x) to be positive and continuous in the intervals of a £ x £ b where length was b-a. He subdivides the intervals by (n-1) at points x1, x2, ···, xn-1 into n equal and unequal intervals. He also provided the sum of the function by letting x0=a, xn=b
The rise of calculus brought a unique moment in mathematics as it developed and invention modern mathematics which required the creation of new mathematical tools such as computers. These two ancient mathematicians; Newton and Gottfried created different methods of dealing with mathematical problems that inspired modern calculus. Together they created mathematical systems that dealt with variable quantities and defined different descriptive terms in describing change (Mates, 1986).
In the 1820s Leibnizian analytical calculus became accepted in English and Leibniz and Newton independently developed basic calculus and Leibniz gave new discipline to today’s calculus. They both influenced the notations used in today’s mathematics. Newton introduced the notation ƒ for the derivative of a function f. To Leibniz, the symbol ∫ represented the integral and wrote the derivative of a function y of the variable x as dx/dx, both of which are still in use today (Mates, 1986).
Integrals
Niels Henrik Abel considered differential expressions to be integrated into a finite form with the aid of ordinary functions. Together with Cauchy, they undertook the general theory of determining definite integrals, a subject which became very popular in 19 century. Through the developments, Frullani’s theorem in 1821, Bierens de Haan’s mathematical theorem of 1862, and elaborate tables of 1867, Meyer’s treaties of 1871, and many others contributed to the development of today’s mathematics.
Euler was the first to study Eulerian integrals as
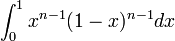
is divided by
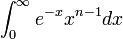
. In his theorem he explained that if n is an integer, then this would apply as;
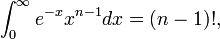
. But the integral converges for all positive real n and defines an analytic continuation of the function to all of the complex planes except for poles at zero and the negative integers. The symbol Γ, which is now called the gamma function. He was analytic over the positive reals, Γ also defined the log Γ as a convex (smith, 2007, p.32).
Symbolic Methods
Symbolic methods were discovered by Taylor; he differentiated the analog between successive differentiation and ordinary exponentials and can be applied algorithmically to solve certain types of problems. In 1800, Arbogast was the first to separate the symbol of operations from a quantity in the differential equation and Francois (1812) and Servois (1814) gave the correct rules of the subject. This method become active when Hargreave (1848) applied it in differential equations such as algebra, geometry, variable quantities, the concept of function, and limit arithmetisation of geometry and notations used in calculus. Boole freely employed all these methods in studying the equations in the theory of complex numbers (Smith, 2007, p.33).
Conclusion
Calculus research reveals that geometers were not interested in polynomials of degrees more than four and were able to use ibn al Haytham’s formula in finding arbitrary integral powers in calculating power series in functions and they also knew how to calculate differentials of functions. We can see that basic ideas of calculus were known to Egyptians and Indians long before Newton came into play but they did not see the necessity of connecting their ideas into calculus.
Newton and Gottfried, though they were not the first people to invent calculus, diligently combined the many ideas which were brought into place by various, into two unifying themes; derivative and integral, and turned calculus into the modern problem-solving tool.
The idea of transmission of mathematical knowledge from one culture to the other is a matter of current research and debate spared for another day. All the Geometers contributed greatly to developing modern mathematics and they should all be credited for their hard work since each one’s of them relied upon their predecessors in developing their formulas. Mathematics has now become the basic entry point for anyone wishing to study finance, economics, and even scientific subjects. It has also simplified today’s life for most scientists since it has made it possible to predict pressure building up behind a dam as the water rises up. The inter-relationship between ancient and modern calculus can be seen in the invention of computers which has provided simpler forms of solving calculus problems that were considered impossible.
References
Aslaksen, H. (2006). Why calculus? Web.
Boglery, W., A. 1996. Calculus Quest. Web.
Connor, J.,J., &Robertson,E. F. (2000). An overview of Indian Mathematics. Web.
Chapter II. The Fundamental Ideas of the Integral and Differential Calculus. Web.
How Archimedes found the Area of a Circle. Web.
Kartz, V., J. (1995). Ideas of Calculus in Islam and India. Mathematica Magazine, 65(3), 1-35
Math pages. Archimedes on Spheres and Cylinders. Web.
Mates, B. (1986). The Philosophy of Leibniz: Metaphysics and Language. Oxford: Oxford University Press.
Smith, E. D. (2007). History of Modern Mathematics. New York: Cosimo books.