Introduction
A sample can be described as a portion of the population selected for a survey or experiment. Obtaining facts regarding a parameter from the entire population is desirable. However, it is often time-consuming and costly, which necessitates sampling (Das, Mitra, & Mandal, 2016). Nonetheless, small samples cause uncertainties in statistical computations and lower the reliability and validity of the outcomes. Therefore, using the correct sample size is key in any research endeavor. The researcher would like to carry out a project that compares the survey results before and after an intervention in the same sample. A paired t-test is to be used to analyze the results. This paper describes the calculation of the sample size and justifies the choice of sample size.
Sample Size Calculation
Before calculating the sample size, it is necessary to establish certain parameters that influence the statistical computation. The researcher intends to use a paired t-test to gauge the effectiveness of the intervention by testing a hypothesis, which means that the level of significance needs to be selected. A p-value of 0.05 is commonly used in most types of research. This value means that there is a 5% chance that the findings are due to chance, implying that the researcher has a 95% probability of obtaining the same outcomes if the study is repeated several times (Arifin & Zahiruddin, 2017).
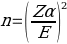 ,
,where n is the required sample size, Z is a constant, σ is the estimated standard deviation that can be obtained from previous trials, and E is the expected error in both directions (forward and backward) (Sullivan, 2017). Z is a constant that is chosen by default based on the accepted α error and whether the test is one-sided or two-sided. The selected α error is 0.05, whereas the test is expected to be two-sided because two outcomes are possible in the hypothesis testing. Therefore, the value of Z for a two-sided test at α= 0.05 is 1.96 (from the Z table) (Brase & Brase, 2016). In the proposed study, it is projected that the standard deviation between the observations will be 5.5 and that the error in both directions will be 0.2.
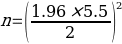 , which is equal to 29.05. This value can be rounded off to 30 subjects.
, which is equal to 29.05. This value can be rounded off to 30 subjects.Justification of Sample Size
When selecting a sample size, it is necessary to ensure that the number is right. A large sample size has negative financial implications and leads to wastage of resources. Conversely, if the sample is too small, it diminishes the statistical power of the study. Power refers to the ability of an investigation to prove traits that exist in the study population (Brase & Brase, 2016). A sample size that is too small raises the chances of having a type II error, which is the possibility of accepting the hypothesis of no difference when a variance exists in the population (Das, Mitra, & Mandal, 2016). Effect size denotes the influence of an intermediation.
Values ranging from 0.5 to 0.8 are ideal because they signify a moderate to high effect size. Conversely, the most acceptable value of power is 80% (Albers, 2017). Statistical power can be employed in gauging the suitability of the sample size.
The choice of the statistical test also justifies why the sample size should be 30. A t-test is used to analyze data when the standard deviation of the population is unknown and is useful for smaller sample sizes of 30 or less (Albers, 2017). However, the standard deviation of the sample should be approximated from experimental trials or published data.
Conclusion
Sampling enables the use of representatives of a population to explain a phenomenon. The key goal of sampling is to obtain a sample that is large enough to perceive a significant effect and small enough to minimize the wastage of resources. The appropriate sample size can be calculated using mathematical formulas provided that parameters such as the expected average, level of significance, and standard deviation are known.
References
Albers, M. J. (2017). Introduction to quantitative data analysis in the behavioral and social sciences. John Wiley & Sons.
Arifin, W. N., & Zahiruddin, W. M. (2017). Sample size calculation in animal studies using resource equation approach. The Malaysian Journal of Medical Sciences: MJMS, 24(5), 101-105.
Brase, C. H., & Brase, C. P. (2016). Understandable statistics: Concepts and methods. Cengage Learning.
Das, S., Mitra, K., & Mandal, M. (2016). Sample size calculation: Basic principles. Indian Journal of Anaesthesia, 60(9), 652-656.
Sullivan, L. M. (2017). Essentials of biostatistics in public health. Jones & Bartlett Learning.