Z-values, also known as standard scores, can be defined as the elements that allow defining whether “the number of standard deviations the original measurement is from the mean” (Brase and Brase “Normal Curves and Sampling Distributions” 62). Herein their significance lies. For the same reason the specified elements do not have any units of measurement – they are used merely for comparing the information acquired in the process of a statistical analysis.
According to Brase, it is highly desirable that, when determining the z-values, one must compare the data sets that feature different units of measurement (Brase and Brase “Normal Curves and Sampling Distributions” 65). While seemingly odd, the specified strategy, in fact, is crucial, as the results may be incorrect otherwise (Brase and Brase “Normal Curves and Sampling Distributions” 66).
Indeed, according of Brase, using solely a mean is not enough to describe the data adequately. The use of the data sets that contain the same kind of information, therefore, poses a threat to the veracity of the results. Still, it is possible to evaluate differences in the quality of performance under a standard curve by converting the scores to a standard normal distribution (Brase and Brase “Normal Curves and Sampling Distributions” 69).
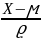 (Brase and Brase “Normal Curves and Sampling Distributions” 65).
(Brase and Brase “Normal Curves and Sampling Distributions” 65).It should be noted that the z-values may be replaced with confidence intervals. The latter provide a range of values that may include an unknown population parameter (Brase and Brase “Estimation” 72). The estimated range, in its turn, is calculated based on the set of sample data provided (Brase and Brase “Estimation” 73). Because of the difference in the sample range of values, the necessity to calculate standard deviation occurs. After the standard deviation is identified, the normal curve is built in order to locate the standard normal distribution. The area under the curve that falls within the interval is identified as the probability produced by the confidence interval (Brase and Brase “Estimation” 74).
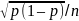 (Brase and Brase “Estimation” 75).
(Brase and Brase “Estimation” 75).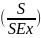 2 (Brase and Brase “Estimation” 75). Thus, the sample size is calculated for a predetermined error tolerance.
2 (Brase and Brase “Estimation” 75). Thus, the sample size is calculated for a predetermined error tolerance.Works Cited
Brase, Charles Henry and Corinne Pellillo Brase. “Estimation.” Understanding Basic Statistics. 6th ed. Stamford, CT: Brooks/Cole Publishing Company, 2012. 72–76. Print.
—. “Normal Curves and Sampling Distributions.” Understanding Basic Statistics. 6th ed. Stamford, CT: Brooks/Cole Publishing Company, 2012. 61–71. Print.