Boyle’s Law: Pressure-Volume Relationship in Gases

Experimental Objectives

• To establish the relationship between the volume and pressure of a confined gas
• To determine mathematical relationship between gas pressure and volume of a gas in a confined system
• To use established mathematical relationship to determine pressure or volume gas when of one of the variable is changes at constant temperature

Theory

According to Fowler, Boyle’s Law states that at constant temperature, the pressure of a given gas is inversely proportional to the volume (1).Boyle discovered that when pressure of a gas is increased by two-fold, the volume of a gas will contract to half its earlier volume at constant temperature. A plot of pressure against volume of an ideal gas at constant temperature gives a negative inclined graph curve, an indication of inverse proportionality. Therefore, in mathematical terms, the relationship can be expressed as,

PV=Constant or PV=k …….. (1)

Where P=pressure of gas, V=volume of gas and k=a constant of proportionality of ideal gas

Boyle’s Law is utilized in calculating changes in pressure and volume at steady temperatures (initial and final pressure and volume). This is calculated using the equation: p₁V₁=p₂V₂… (2)

Where: p₁=initial pressue, V₁=initial volume, p₂=final pressure and V₂=final volume

DATA and calculations

From the data obtained, a graph of pressure against volume was plotted. Additional, another graph of pressure against reciprocal of volume was drawn as shown below:

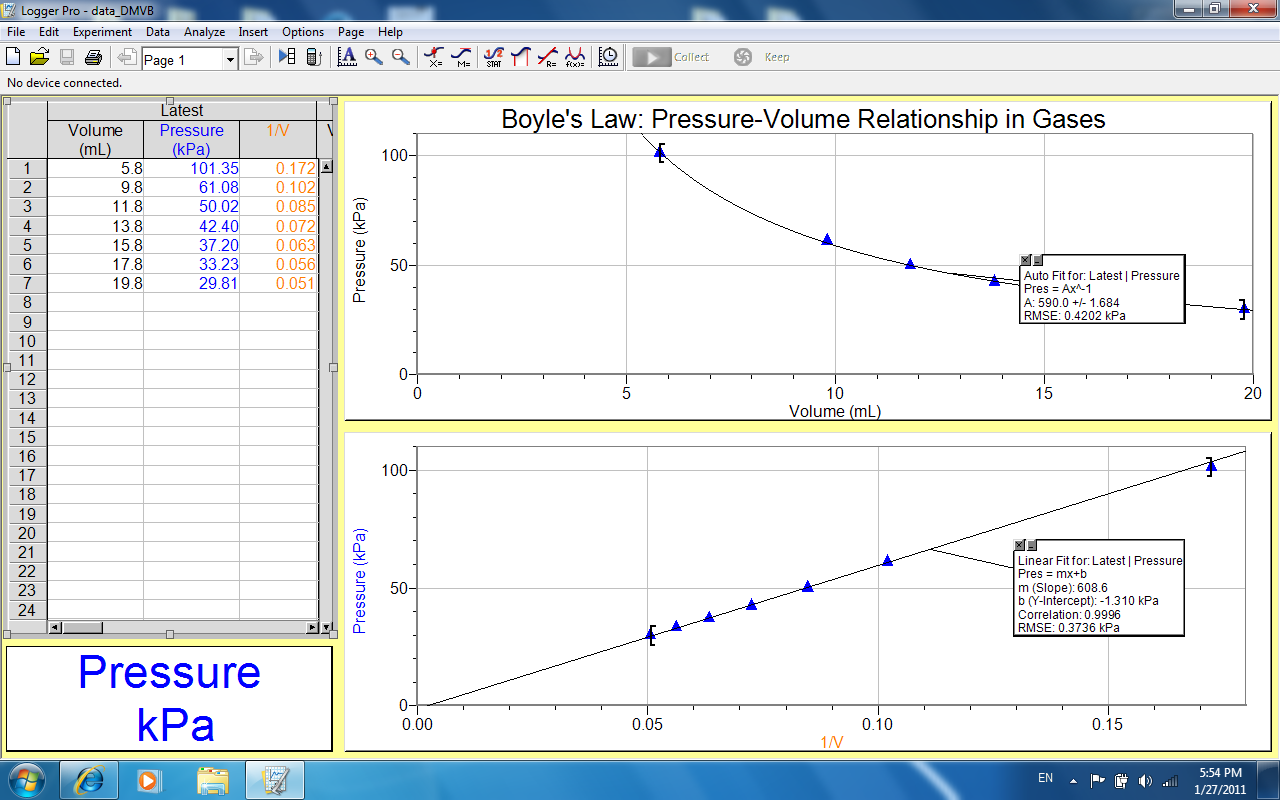
Discussion

From the graph, we see that when volume of a gas is increased, the pressure of the gas decreases proportionally i.e. when volume is doubled, pressure of the gas is halved. From the experiment, when volume of the gas from increased from 5.8ml to 15.8ml, pressure decreased from 101.35kPa to 37.20kPa. This evident from the graph where pressure was plotted against volume at constant temperature, it gave a negative inclined graph curve, an indication of inverse proportionality.

Conclusion

Since a plot of pressure vs. volume gives a negative inclined a graph, it shows that pressure and volume at constant temperature are inversely related and they are represented by the equation: PV=Constant or PV=k. Boyle’s law was verified and therefore the objectives of the experiment were achieved.

Data processing Questions

1. From the data obtained, when the volume of the gas is doubled, the pressure of the gas is halved i.e. when volume was increased from 5ml to 10ml pressure decreased from 101.35kPa to 55.19 kPa. Value is not exactly half due to deviation from ideality by the gas.
2. When volume is halved from 20.0 mL to 10.0 mL, data shows that pressure doubles i.e. it increases from 28.78kPa to 55.19kPa.
3. Data shows that when volume is tripled, pressure decreases by a third i.e. pressure decreases from 101.35kPa to 37.20kPa
4. From the results in the first three questions, the relationship between the pressure and volume of a confined gas is inverse proportional. We see that when volume of the gas is tripled from 5.8ml to 15.8ml, pressure decreases by a third from 101.35kPa to 37.20kPa. On the other hand, when volume of a gas is halved from 20.0 mL to 10.0 mL, data shows that pressure doubles i.e. it increases from 28.78kPa to 55.19kPa. In addition, the graph is a negative inclined one a clear indication of inverse relationship between pressure and volume. therefore we can conclude that pressure and volume are inverse proportional at constant temperature
5. We apply the equation, p₁V₁=p₂V₂ where , p₁=37.20kPa, V₁=15.8ml , V₂=40ml and p₂=unknown and substituting respective values,
   37.20X15.8=40X p₂
   p₂=14.694kPa
   We see that when volume is increased to 40ml, pressure will decrease to almost half of that when volume is 19.8ml.
6. When volume is decreased to 2.5ml, applying the equation , p₁V₁=p₂V₂ where p₁=101.35kPa, V₁=5.8ml , V₂=2.5ml and p₂=unknown and substituting respective values, 101.35X5.8=2.5X p₂
   p₂=235.13kPa
   We see that when volume is decreased to 2.5ml, pressure doubles to give 235.12 kPa.
7. Temperature is kept constant
8. The relationship is inverse and therefore I have multiplied and tabulated in column 3(k=Vp)
9. The value of k was fairly constant and fell between 585.12 and 591.49. There was is minor variations, which can be attributed to experimental errors and deviation of the gas from ideality.
10. Boyle’s law can be expressed as PV=k. Boyle’s law states that at constant temperature, volume of an ideal gas is inversely proportional to the pressure gas.

Reference

Fowler, Michael. “Boyle’s law and the law of atmospheres.”Galileo Physics Journal, 12(2006):1-7