Introduction
Complexity theory is closely linked to chaos theory, this theory studies systems that are very complex to precisely forecast their future, but nonetheless show fundamental patterns which can assist us to deal with this increasingly complex world. Science typically examines the world by breaking it into smaller and smaller pieces so as to understand the pieces. Many times the use of this approach leads to missing the bigger image.
For example, “knowing all possible information about an individual ant will not educate us about how a whole ant colony works”. So does dissect a mouse will by no means tell us all we require to know about living mice. According to Waldrop (1992), Complexity study is the science of “non-linear dynamics”. That terminology clearly suggests that there ought to be some use in the investigation of communication.
Occasionally the manner in which the parts interrelate is vital to how the entire system works. Complexity studies this aspect. Complexity is appropriate to a vast range of aspects of the study which includes earthquakes, traffic flows, the stock market, airline networks, Jupiter’s red spot, group dynamics, the internet, spread of viruses, urban planning, and much more. Complexity Theory and chaos theory are modern sciences, which only actually developed ever since the start of computers capable of undertaking the enormous computations essential to discover the mysteries of complexity. As Prof. Stephen Hawking states, “The next century will be the century of complexity”. Several concepts applied in Complexity studies have moved into the mainstream application, for instance, tipping points, six degrees of separation, and the butterfly effect. (Waldrop, 1992)
Overview
Complex behavior has been observed in the laboratory in diverse systems which include lasers, electrical circuits, fluid dynamics, oscillating chemical reactions, and mechanical and also magneto-mechanical devices. Morrison, (2002) states that complex behaviors can also be observed in nature, this includes the time evolution of the magnetic field of celestial bodies, the dynamics of satellites in the solar system, population growth in the ecosystem, molecular vibrations, and the dynamics of the action possibilities in neurons. Daily cases of complex systems include climate and weather.
Systems that show mathematical chaos can be determined and therefore systematic in some way. The technical application of the term chaos is at odds with ordinary phraseology, which suggests total disorder. As well as being organized in the feeling of being able to be determined, complex/chaotic systems typically have sound defined statistics. For instance, the Lorenz system is complex /chaotic; however, it has an undoubtedly defined structure. (Morrison, 2002)
A short History
In spite of early insights in the first part of the 20th century, complex theory became formal as such only past mid-century, after it became clear for a number of scientists that, linear theory, the existing system theory at that particular time, basically could not clarify the practical behavior of some experiments like that of the logistic map. What had been beforehand excluded as measure imprecision and simple “noise” was considered by chaos theories as a full component of the studied systems. (Badii & Politi, 1997)
The most important vehicle for the advancement of complex theory was the electronic computer. A great deal of the mathematics of complex theory entails the repetitive iteration of plain mathematical formulas that would be not practical to do manually Electronic computers enabled these repetitive calculations to be practical, whereas images and figures made it achievable to visualize these very systems. ENIAC, one of the initial electronic digital computers, was used in running uncomplicated weather forecasting models. (Badii & Politi, 1997)

The picture above shows Turbulence in the tip vortex from an aircraft wing.
A study of the critical point past which systems create turbulence was imperative for complex theory, examined for instance by Lev Landau a Soviet physicist who developed “the Landau-Hopf theory of turbulence”. David Ruelle and Floris Taken afterward made a prediction, against Landau, by predicting that fluid turbulence could develop through an odd attractor, the main concept of complex theory. (Gollub& Baker, 1996)
Complexity types
Complexity Theory takes the observation that systems should be best considered as wholes, and study as such, discarding the customary importance of simplification and reduction as insufficient practices on which to put a basis such scientific work. Such techniques, while important in analysis and data compilation, fall short in their function at the system level owing to the intrinsic nonlinearity of powerfully interconnected systems since the effects and causes can not be separated and the whole can not be the sum of the individual parts.
The approaches applied in the complexity theory are founded on several new mathematical techniques, which originate from fields as varied as physics, biology, politics, artificial intelligence, and telecommunications. This interdisciplinary point of view is the critical aspect, reflecting the common applicability of complexity theory to systems in all fields. (Sipser, M, 2006)
Static Complexity (Type 1)
This is the simplest type of complexity, which is generally studied by mathematicians and also scientists; static complexity is associated with fixed systems. The assumption that is made here is that the structure being studied does not vary with time, thus one can approach the examination of the particular system analogously to a photo. For instance, we can examine a computer chip and view that it is complex (in the accepted sense); we can then relate this to a circuit drawing of the electronics and contrast the alternative systems to decide relative or computational complexity, (such as a number of transistors).
Dynamic Complexity (Type 2)
When a fourth dimension is added, in terms of time, it improves and also worsens the condition. On the good side, we can possibly recognize function in sequential patterns a lot more easily than in spatial ones. However equally by permitting components to vary, we may lose those spatial sequences we initially identified, groupings and classifications change with time. (Sipser, M, 2006)
Evolving Complexity (Type 3)
Going past repetitive thinking leads us to a category of a phenomenon generally illustrated as organic. The well-known cases of this relate to the neo Darwinian Theory of Natural Selection, whereby systems evolve with time into dissimilar systems (for example an aquatic form evolves to become land-dwelling). Thus, this open-ended type of change attests to be far more widespread than formerly thought. (Sipser, M, 2006)
Self-Organizing Complexity (Type 4)
The last form of a complex system is which is believed to encompass the very interesting type and which is most applicable to complexity theory. In self-organizing complexity, the internal constraints of closed systems (machines) are combined together with the imaginative evolution of open systems (people). In this perspective, a system is regarded as co-evolving with its surroundings, a lot, so that classifying systems alone, out of context, are not viewed as adequate for a legitimate description. System functions must be described in terms of how they interrelate to the wider external world. (Sipser, M, 2006)
Complex adaptive systems
One of the main focuses of complexity theory is the complex adaptive systems. However, it is not very apparent how complexity is defined, for example, several writers describe a snowflake as “complex’, while others describe it as “merely complicated”. Nonetheless, Holland considers the following to be the key features of any complex adaptive systems: (Badii.& Politi, 1997)
- Various agents act in parallel in a surrounding formed by their connections with other agents in the same system; since the agent is continuously acting and reacting to the other agent’s actions, and nothing in its surroundings is fixed
- Control is greatly dispersed, consequently, any rational behavior that might there in the system has to occur from the competition and also co-operation amongst the agents present
- Numerous levels of the group, agents at one point serving as building blocks for the next point up
- Regular reorganization of the building blocks as an outcome of learning, experiences, evolution, and adaptation
- All the system predicts the future to various degree, making efforts at forecasting on the foundation of models of their surroundings
- All have niches they can exploit, filling up one niche often opening up new ones that can be exploited
- The system never attain equilibrium
- The system can improve on a number of dimensions, except they never optimize
- The richness of the relationships inside the system permits the system as a whole to experience spontaneous self-organization
Sensitive dependence on initial conditions – the ‘butterfly effect’
A butterfly flapping its wings past Cuba in September might influence the path of a tornado heading for Florida in October. Almost all things and each one in the whole world is caught up in an enormous nonlinear network of inducements and constraints. The slightest variation in one place leads to tremors elsewhere. Under the correct situations, the smallest amount of uncertainty can grow up until the system’s future becomes completely unpredictable or chaotic.
Yet, this “butterfly effect” is normally linked to Edward Lorenz, who was using computers in modeling meteorological systems in 1961. One day Edward Lorenz wanted to take a closer examination of one specific sequence on an earlier printout. Rather than starting a run of all the printouts over again, Lorenz simply keyed the data from halfway through the printout. He then set the computer running and then went off to take a cup of coffee. When Lorenz returned he found out that the results were entirely dissimilar from the first printout. The “weather” had been developed in a completely different manner. On re-examining the data, he recognized that he had keyed in.506 as his opening value, while he was supposed to have entered.506127. Lorenz had assumed that such a minor difference would not make any difference. In reality, the dissimilarity was such that he may as well have keyed a randomly chosen figure. (Source: Gleick (1987)
It may thus happen that little variations in the initial condition create very great variations in the final phenomenon. A tiny error in the previous will turn out an enormous error in the final. Forecasting becomes not possible, and thus it leads to the fortuitous phenomenon. (Smith, 1998)
Complex dynamics
In order for a dynamical system to be categorized as complex, it should have the following features;
- It has to be sensitive to the initial condition
- It has to be topologically mixing
- Its periodic orbits have to be dense.
Sensitive to initial condition
Being sensitive to initial conditions implies that every point in that particular system is randomly closely approximated with other points which have considerably diverse future trajectories. Consequently, a randomly small perturbation of the current trajectory may possibly lead to considerably unusual future behavior.
Sensitivity to initial conditions is also popularly termed as the “butterfly effect”, so known as a result of the title of a paper given in 1972 by Edward Lorenz to the American Association for the Advancement of Science in Washington, D.C. the paper was entitled “Predictability: Does the Flap of a Butterfly’s Wings in Brazil set off a Tornado in Texas?” The flapping wing here represents a minute change in the original condition of a particular system that leads to a chain of proceedings causing the large-scale phenomenon. If the butterfly had not flapped its wings, it is possible that the course of the system may have been greatly different. (Smith, 1998)
Sensitivity to initial conditions is frequently confused with complexity in accepted accounts. Sensitivity could also be a fine property, as it depends on the selection of metrics or the idea of distance in the time-space of the specific system. For instance, think about a simple dynamical system created by repetitively doubling an original value (defined via the mapping on the actual line from x to 2 xs). Thus the system will have a sensitive dependence on original conditions everywhere because any pairing of close-by points will finally become broadly separated. Nevertheless, the system has very simple performance, as all points except for 0 lean-to infinity.
But if on the other hand, we apply the restricted metric on the line that is obtained through adding the point at infinity and sighting the end result as a circle, the system will no longer be sensitive to initial conditions. It is for this reason, that in defining complexity, attention is usually restricted to systems with restricted metrics, or closed, restricted invariant subsets of unrestricted systems. (Smith, 1998)
Attractors
A number of dynamical systems are complex everywhere however in a lot of cases complex behavior is present only in a division of phase space. Some cases of a lot of interest occur when the complex behavior occurs on an attractor, as then a great set of original conditions will result in orbits that congregate to this complex region. A simple approach to visualize a complex attractor is, to begin with, a spot in the basin of attraction of the attractor, then just plot its successive orbit. As a result of the topological transitivity conditions, it is most likely to create a picture of the whole final attractor. (Waldrop, 1992)
For example, in a system that describes a pendulum, its phase space may be two -dimensional, which consists of information concerning the position and velocity. An individual may plot the point of a pendulum alongside its velocity. A pendulum not moving will be plotted as a spot, and that in periodic movement will be plotted as a plain closed curve. Once such a plot outlines a closed arc, the curve is known as an orbit. The pendulum will have an infinite number of those orbits, which will form a pencil of nested ellipses in relation to the origin. (Waldrop, 1992)
Strange attractors
Though the majority of the motion kinds stated above offer very simple attractors, for instance, points and circle-like curves known as limit cycles, complex motion results in what is recognized as strange attractors, these are attractors which can have vast detail and complexity. For example, an effortless three-dimensional form of the Lorenz weather system results in the prominent Lorenz attractor. Lorenz attractor is possibly among the well-known complex system diagrams, possibly since not it was one of the first, and also one of the very complexes, thus it rises to be a very interesting pattern that looks akin to the wings of a butterfly. The Rossler map is an additional such attractor, which experiences period-two doubling course to turmoil, same as the logistic map. (Waldrop, 1992)
Strange attractors happen in both constant dynamical systems (for example Lorenz system) and also in some distinct systems (for example the Henon map). Other distinct dynamical systems encompass a repelling structure known as Julia set that occurs at the border amid basins of attraction of preset points. Julia sets can be taken as odd repellers. Together strange attractors and also Julia’s sets naturally encompass a fractal structure.
The Poincare-Bendixson concept indicates that a strange attractor only arises in a continuous dynamical system when it has got three or additional dimensions. But, no such limitations occur to discrete systems that can show strange attractors in two or even one-dimensional systems. (Sipser, 2006)
Computability and complexity
A fundamental field of academic computer science is complexity theory, which involves the examination of the resources required to resolve computational problems. Scientists in this field describe computational concepts, such as Boolean circuits, Turing machines, parallel random access machines, and many more. And resource measures for example space, amount of hardware, parallel time, etc. In many cases, a complexity class is then a set of problems that can be solved in a specific model under specific resource constraints. Such models have to be easy enough to permit mathematical examination yet general enough to be helpful in a broad context. (Sipser, 2006)
Here is a diagram of the world of computability and complexity:
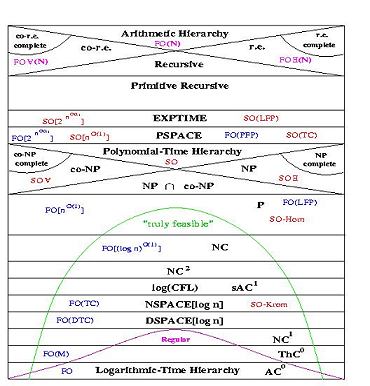
Possibly the most difficult thing to confirm about a computational concept is that it was not able to solve a specified problem inside particular resource limitations. Such “lower bounds” are presently obtainable if only when the concept is very specialized or when the limitations are very severe. (Sipser, 2006)
Conclusion
Complexity theory makes an observation that systems should be best considered as wholes, and be studied as such, discarding the traditional significance placed on simplification and reduction as insufficient practices on which to put a basis such scientific work. In the words of Sipser (2006), he states that “Complexity Theory is critically interacting components self-organize to form potentially evolving structures exhibiting a hierarchy of emergent system properties”. In any fresh scientific activity, it is important to have a focal point with which to focus the mind, and also to encourage comprehensive work. The general foundations of complexity theory are at present quite well established. Thus it is clear that the theory’s importance and contribution will continue to increase in the value of more studies being done. Complexity theory’s importance in the world of science as such remains certain.
Reference:
Badii, R & Politi A. (1997): Complexity: hierarchical structures and scaling in physics”. Cambridge University Press.
Gollub, J. P& Baker, G. L. (1996): Chaotic dynamics. Cambridge University Press.
Morrison, K. (2002): Complexity theory; School leadership and complexity theory. Chapter 1, 5-31. London: Routledge Falmer.
Sipser, M (2006): Time Complexity, Introduction to the Theory of Computation, 2nd edition, USA: Thomson Course Technology.
Smith, P (1998): Explaining Complexity, Cambridge University Press.
Waldrop, M.M (1992): Complexity; the Emerging Science at the Edge of Order and Chaos, Simon & Schuster.