Enzyme- and Acid-Catalyzed Hydrolysis of Glycoside Salicin

Introduction

Background

According to BCS (1996) interpretation of catalysis reactions can be carried out using transition state theory. The process of converting reactants into products involves formation of intermediate products that dissociate to form final products. in a non-directed reaction, a side reaction can result leading into formation of side products (side products are products of a reaction that occur but are not the intended products).

Brito-Arias (2007) indicate that in some reactions, the formation of an intermediate compound is not favoured due to physical conditions of the reactions whereas in some cases the intermediate complex formed is stable and establishes an equilibrium state with the reactants. In the case of a stable intermediate product, there are no products that are formed unless efforts are made to overcome the activation energy required to realize the transition state for the products to be formed from decomposition or rearrangement of the intermediate products. Some of organic intermediate compounds formed occur such that the intermediate compound becomes neutral and no migration of electron could occur.

This halts the reaction. Another scenario that can bring an organic reaction to a stand still is when the nucleophile, which is the electron source has an electron withdrawing group at ß carbon atom (IUPAC, 1997a). such a scenario is observed in α-ß-keto esters that require oxo-insertion in order to form a nucleoplhile that can deprotonate a hydronium ion leading into formation of a protonated α-ß-keto ester hence realizing an electron sink at the α-carbon atom to the carbonyl functional group.

The electron withdrawing group reduces electron density at the electron source and the nucleophile becomes electronically neutral. Another scenario is when the electrophile has an electron donating group on ß-carbon atom. The electron donating group donates electron to the deficient electron sink hence stabilizing the molecule. A reaction cannot therefore proceed if the reactant is electronically neutral because no electron transfer can occur. The reaction can only be achieved through introduction of better leaving groups (IUPAC, 1997b).

Aims of the experiment

1. To carry out an acid –catalyzed hydrolysis of glycoside salicin and determine absorbance as a function of time.
2. To carry out enzyme catalysis of glycoside salicin and use data on absorbance at 290nm at various time intervals to determine the first order rate constant for the reaction
3. To isolate emulsin from almonds and carry out comparative studies on its efficiency compared to standard catalysis.

Literature review

Laidler (1997) indicates that Activation Energy, denoted as Ea, is the energy required to convert reactants to transition state of the reaction. Transition state is the reaction’s highest energy profile or the energy barrier for the reaction (Laidler, 1993). Increasing temperature has been established to help in breaking the transition state of a reaction because it increases vibrational energy of the molecules and rate of collision of the molecules. In biological systems, increasing temperatures or use of finely divided catalysts is not possible because body reactions occur at very narrow temperature conditions for reactions (Ingle & Crouch, 1988).

Bugg (2004) provides that enzymes are biological catalysis that help to lower activation energy of the chemical reaction pathway. Hence enzymes create a reaction pathway that has lower activation energy for the reaction to occur.

Chemical kinetics provides that for an acid catalyzed reaction, the rate of hydrolysis is directly proportional to concentration of the substrate and the acid used for the hydrolysis (Laidler, 1993).

Hence

Rate = (-dx/dt clX [H+]………equation 1

Where x is concentration of the substrate

The negative sign indicates that the concentration of the substrate decreases as time increases. But the acid is only used for protonation purposes so that a better leaving group could be formed at the electron sink. This means the concentration of the acid remains constant through out the reaction because it is not involved in formation of any product (Page and Williams (1987). This implies

Rate = -dx/dt = kx …..equation 2

This results into a graph that passes through point zero of the vertical and horizontal axis with a gradient of k)

The reaction therefore follows a pseudo first order kinetics because the rate of the reaction depends on one reactant. In measuring the concentration of the products of the hydrolysis, the concentration of the phenyl-derivative is determined. This implies that at time t=y, we have

Y = a – x …..equation 3

This means at the end of the reaction, if no equilibrium is established, the concentration of the phenyl-derivative will be equal to the concentration of the glycoside derivative (Warshel, 1991). Hence

ln( a –y/a) = kt

According to Beer Lambert law, A =εcl

Where:

A= absorbance

ε=extinction coefficient

C= concentration in moles /Litre

L= length of the cell in cm

By deduction, it follows that concentration of phenyl-derivative (thus y) will be proportional to the absorbance at 290nm because ε and l are constants.

Hence

Ln (A_∞ -A) = -kt + ln A_∞

Since all enzymes at any point of reaction exist in form of an enzyme-substrate complex, the rate is represented by

Rate = -dx/dt k since concentration of enzyme is a constant then –dx/dt = k, whose integral is zero meaning the reaction is a zero order kinetic whose units are Ms-1. Ahhrenius equation of reaction relates to rate constant K as a function of Ea. Where

ln k = -Ea/RT + ln A

Where R is the gas constant (8.314 J/mol^-1k^-1)

T is the absolute temperature

A is the frequency factor. If the rate is determined at two different temperatures thus T₁ and T₂, then

Ea = RT₂T₁ ln(K₂/K₁)/T₁-T₂ …….equation 4.

Methodology of the experiment

Procedure: experiment A

Reagents used for the reaction

• Phosphate buffer at PH 6, Concentration = 0.1 M
• Solution E (0.67g dissolved in a phosphate buffer in 250 ml conical flask)
• 2M NaOH
• Solution F (0.005g emulsion in phosphate buffer -10ml

Apparatus used during the reaction

• Thermostated Water bath at 30oC
• Thermostated Water bath at 40oC
• Fourteen 100 ml test tubes
• Thermometer
• Stirrer
• Four significant figure digital balance
• Four 100 ml Measuring cylinder
• Four 10 ml measuring cylinder
• Fourteen pipettes

Procedure A

Procedure 1 of the reaction

• Mix 7.5 ml of salicin solution E and 2.5 ml of emulsin solution F in a 50 ml conical flask at 30oC.
• Record the time of mixing
• At time zero (time of mixing), pipette 0.3 ml of the mixture and add it into test tube containing 2M NaoH
• Repeat the procedure of pippeting 0.3 ml of the mixture six more times at an interval of 3 minutes.
• Label every test tube and keep it in a test tube rack or test tube holder

Procedure 2 of the reaction

Repeat procedure 1 on the 40oC water bath for the rest of seven test tubes

Procedure 3 of the experiment

Determine the absorbance at 290nM, of all the 14 test tubes against a blank of 7.5 mL NaoH (2M) and 2.5 mL of distilled water.

Deliverables

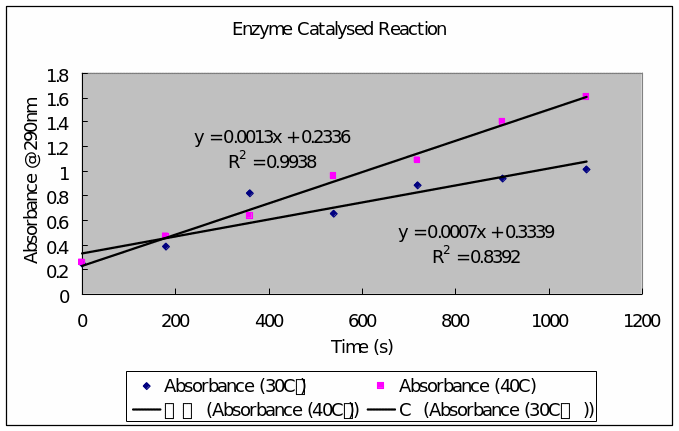
• A plot the graph of absorbance (vertical axis) against time (horizontal axis) and calculate zero order rate constants
• Determination of Energy of activation, Ea, for the enzyme catalyzed reaction

Procedure B

Reactants used

Concentrated Hydrochloric acid

• 2M NaoH
• Solution G (solution of salicin prepared from 0.67g in aqueous 1-propanol (80% water and 20% 1-propanol)

Apparatus used

• A thermostated water bath at 65^oC
• A thermostated water bath at 75^oC
• Fourteen test tubes containing 10mL of 2M NaoH
• 100 ml Test tubes
• 10 ml test tubes

Procedure 1 of the experiment

• Mix 7.5 mL of the Salicin solution G with 2.5 mL of concentrated HCL in a 50 Ml test tube in a 65^oC water bath
• Cover the 50 ml flask with a parafilm
• Pipette 0.3 ml aliquot at time zero
• Quench the 0.3 ml with excess of 2M NaoH
• Mix with vortex mixer
• Repeat the above steps for 6 other aliquots at an interval of five minutes

Procedure 2 of the experiment

• Repeat the above steps in procedure 1, procedure B, using the 75^oC water bath.
• The time interval between every aliquot pipette should be three minutes

Procedure 3 of the experiment

• Determine T∞ reading by pippetting 0.3 ml of the aliquot by adding it into a test tube labeled 15
• Add 10 mL of 2M NaoH solution

Deliverables for procedure B

• Tabulation of test tube number
• Tabulation of time
• Tabulation of absorbance (At)
• A∞ – At differences (by subtracting absorbance reading from the value obtained in test tube labeled 15
• ln A∞ – At values
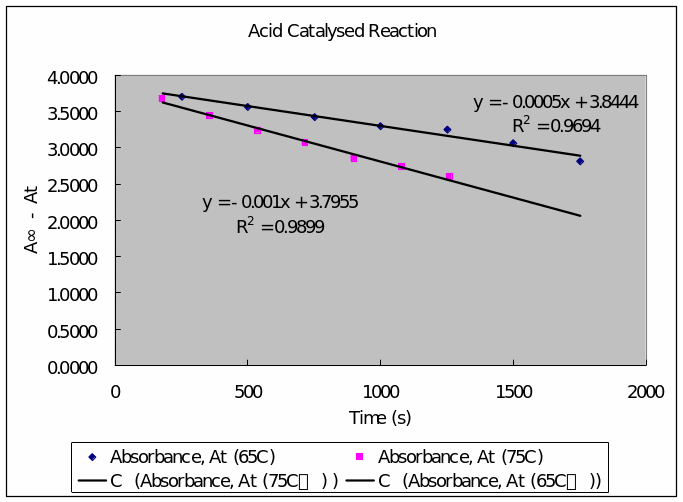
• Plot of absorbance (vertical axis) against time (horizontal axis
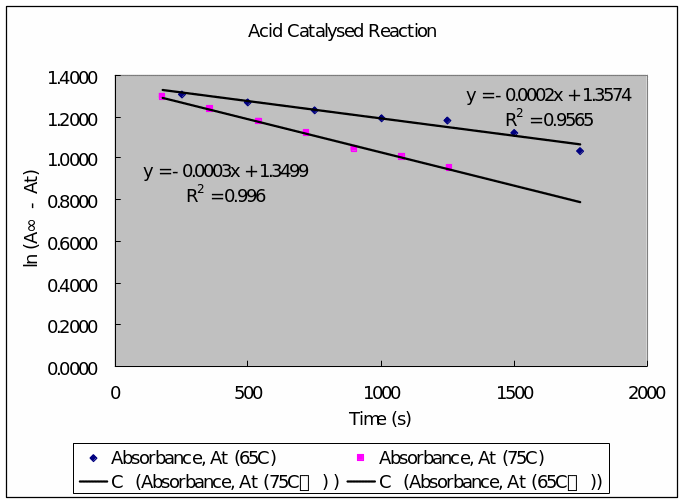
• Plot of ln A∞ – At (vertical axis against time (horizontal axis)
• Determination of the first order rate constant
• Determination of Energy of activation for the acid-catalyzed reaction

Method 3 for the isolation of Emulsin from Almonds

Procedure for the method 3

• Place two almonds in boiling water for 15 seconds
• Pour out the water
• Peel off the green skins
• Grind the ‘blanched’ almonds using mortar and pestle
• Add 10mL of water and grind into a paste
• Add 10mL of 10% acetic acid to coagulate present proteins
• Let it to settle for 10 minutes
• Stir at interval of 2 minutes for four minutes
• Filter half of the solution using a fluted filter paper
• Add 1 drop of 10% acetic acid to the filtrate to clear the filtrate
• (Add dropwise 10% acetic acid until the filtrate clears if it does not clear with the first drop)
• The filtrate is now assumed to contain the emulsin protein

Procedure 2 of the experiment

• Prepare two test tubes each containing 10 ml of 2M NaoH (one of them should be labeled as standards while the other should be labeled as emulsin)
• For the standard test tube mix 7.5 mL of Salicin solution E , 2.5 mL of distilled water and one drop of 10% acetic acid
• For the emulsin test tube, mix 7.5 mL of salicin solution E, 2.5 mL of the filtrate and one drop of 10% acetic acid
• Incubate both test tubes at 40oC for ten minutes
• Pipette 0.3 ml aliquots
• Quench the reaction by adding excess of 2M NaoH
• Determine absorbance at 290 nM for the two tubes against a blank of 7.5 mL 2M NaoH and 2.5 mL of distilled water.

Deliverables

• Comment on the results.
• Explanation on whether almonds contain very much emulsin and reason for the answer.

Results presentation

Wavelength = 290nm

Enzyme Catalyzed Reaction

Table 1: enzyme catalyzed reaction in a water bath thermostated at 30 Cﾟ (at a three minute interval between aliquots)

Table 2: enzyme catalyzed reaction in a thermostated water bath at 40 Cﾟ (in three minute aliquot intervals)

Acid Catalyzed Reaction

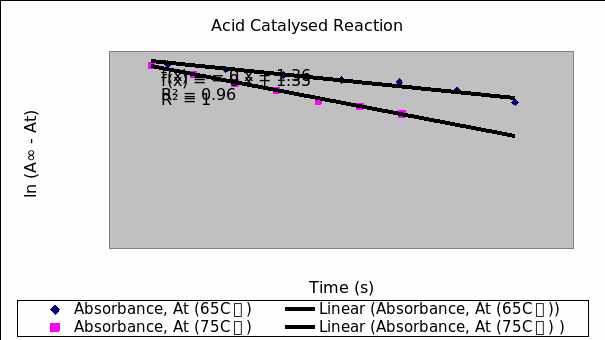
Table 3: acid catalyzed reaction for hydrolysis of the glycoside salicin at 65 Cﾟ (between five minute aliquot intervals).

Table 4: Reaction of the acid catalyzed reaction for the glycoside salicin at 75 Cﾟ.

Almond does not contain as much salicin as the standard sample. This is because almonds enzyme is not pure and exists as a mixture of other compounds and there are other chemical compounds that affect it reactivity rates as opposed to the standard.

Table 6: tabulation for time, absorbance, A∞-At, ln (A∞-At) at 65oC and 75oC.

Conclusion

The enzyme catalyzed hydrolysis of glycoside salicin occurs at faster rate that the acid-catalyzed reaction. This is because the enzyme catalyzed reaction has lower activation energy. The reaction pathway established by the enzyme has a lower transition state hence lower activation energy and a fast rate of reaction. The almond does not contain as much concentration of enzyme as the standard because it exists as a mixture. Another factor that could have contributed to lower activity of the almond derivative could be possibilities of denaturation of the enzyme following heating. Enzymes, being protein in nature are denatured at elevated temperatures.

Future studies should therefore investigate reactivity trends of enzymes whose side groups either have electron donating groups and electron withdrawing groups so that control enzymes can be developed with either electron withdrawing or donating side groups. Further research work should be carried out on effects of protecting the reactive side groups with either neutral, electron withdrawing group or electron donating groups in order to determine the rates of reaction of an enzyme.

Questions

What do you conclude from your results for the activation energies for the enzyme – and acid – catalyzed reactions?

The activation energy of the enzyme catalyzed reaction is lower and therefore occurs at a higher rate.

Give a mechanism for a acid-catalyzed hydrolysis of salicin 1

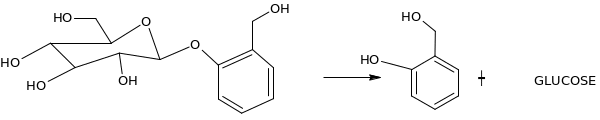
The mechanism of the reaction

In question 2, would you expect the initially formed product glucose to be the α-anomer or ß-anomer? Explain your answer.

The initially formed product is a ß-anomer. This is because it is a product of a ß-glucose derivative. Condensation of ß-glucose gives rise into a ß-polysacharide. It follows immediately that hydrolysis should yield its starting monomers. Due to electron density, ß-anomer glucose will not be stable and undergoes rearrangement to form α-anomer that is relatively stable and is not subject to electron density that could stimulate rearrangement.

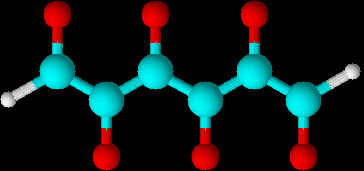
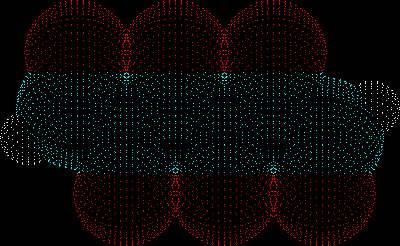
Whole three dimensional electron cloud is represented by

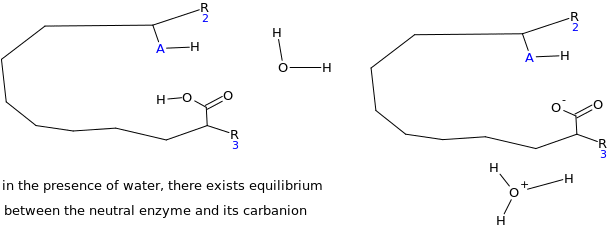
Assuming the emulsion salicin complex has the following general structure (HA=acidic group) suggest a mechanism for the enzyme catalyzed reaction (Hint water is present)

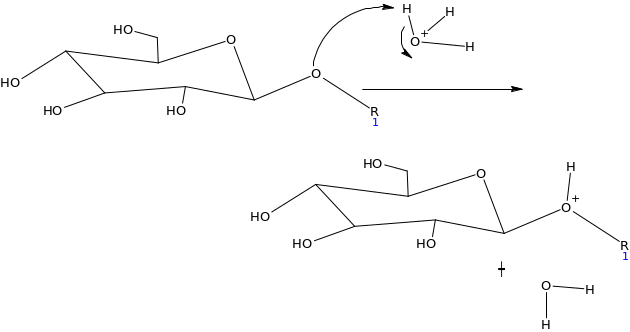
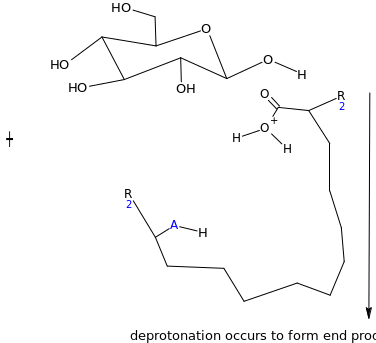
Suggest some reasons why this process should be so much efficient than the acid catalyzed reaction?

The enzyme-catalyzed reaction is a more efficient process because it is a forward reaction but the acid-catalyzed reaction is not efficient in terms of products or yield because at every step of the reaction, the reaction establishes a state of equilibrium. This means the enzyme –catalyzed reaction gives into a larger yield compared to the acid-catalyzed reaction.

The reaction of the enzyme-catalysis of the glycoside occurs at a lower temperature with more efficiency than the acid-catalyzed reaction

The enzyme-catalyzed reaction occurs at lower activation energy. Products are therefore formed faster than in the acid-catalyzed hydrolysis.

In question 4, would you expect the product glucose to be α-anomer or ß-anomer? Explain your answer.

The initially formed product is a ß-anomer. This is because it is a product of a ß-glucose derivative. Due to electron density, ß-anomer glucose will not be stable and undergoes rearrangement to form α-anomer that is relatively stable and is not subject to electron density that could stimulate rearrangement.

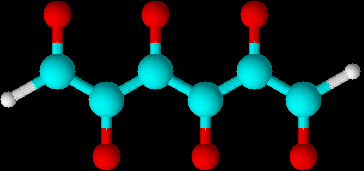
Whole three dimensional electron cloud is represented by

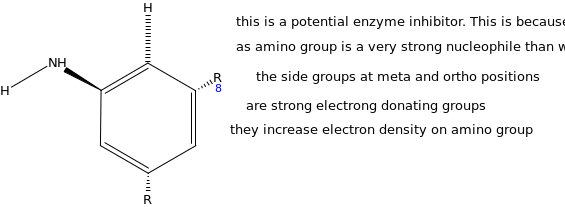
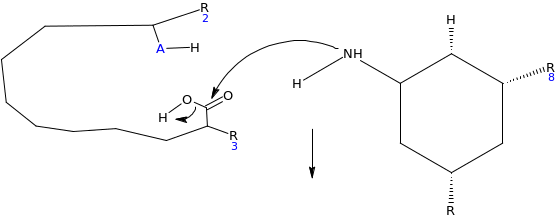
Based on the transition state for the enzyme catalyzed reaction, design a potential enzyme inhibitor. Explain how it works.

The potential enzyme inhibitor

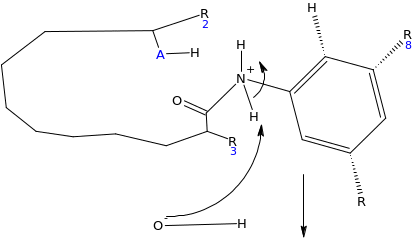
Mechanisms through which the enzyme inhibitor works

At equilibrium

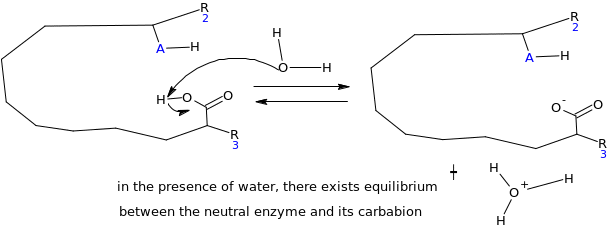
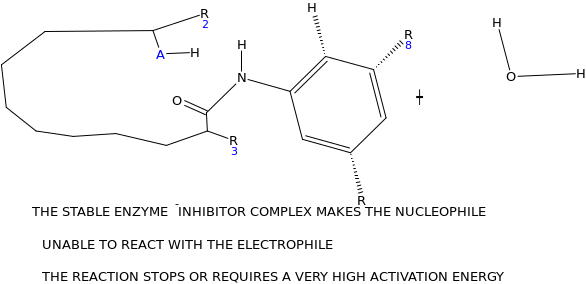
When the inhibitor is introduced, lone pairs of electron on the amino group react with the carbonyl carbon on the carboxylic end, as the electrophile, which results into elimination of the hydroxyl group (OH). This locks the active site of the enzyme. Since the enzyme is the electrophile to the glycoside salicin which acts as nucleophile, there is no possibility of reaction taking place.

List of reference

Biological and Chemical Sciences (BCS) -University of London, 1996, 2-Carb-33: Glycosides and glycosyl compounds, Biological and Chemical Sciences, University of London.

Brito-Arias, M. 2007, Synthesis and Characterization of Glycosides, New York: Springer.

Bugg, T., 2004, introduction to enzymes and C0-enzymes chemistry, 2^nd edition, Blackwell publishing limited.

Ingle, J.D. and Crouch, S.R. 1988, Spectrochemical analysis, New York, Jersey, Prentice Hall.

International Union of Pure and Applied Chemistry (IUPAC), 1997a, Glycosides, IUPAC Compendium of Chemical Terminology, 2nd edition, editors A. D. McNaught and A. Wilkinson. Oxford: Blackwell Scientific Publications.

International Union of Pure and Applied Chemistry (IUPAC), 1997b, Glycosol group, Compendium of Chemical Terminology, 2nd edition, editors A. D. McNaught and A. Wilkinson; Oxford: Blackwell Scientific Publications.

Laidler, K., 1997, Chemical kinetics, 3^rd Edition, Benjamin Cummings.

Laidler, K.J. 1993, The world of physical chemistry, Oxford University Press.

Page, M.I. and Williams, A., (eds) 1987, Enzymes mechanisms, Royal Chemical society.

Warshel, A., 1991, computer modeling of chemical reactions in enzymes and solutions, John Wiley and sons.