Enzyme Determination of Glucose

Introduction

The experiment was conducted to determine the usage and purpose of spectrophotometer relative to Beer and Lambert’s law. Spectrophotometer is used in measuring the intensity of light absorption as described in Beer and Lambert’s law. In the experiment, Glucose and enzymes were provided and since glucose is not absorbent, it was transferred to an absorbent substance through the use of the subsequent equation.

In the experiment, glucose was transferred to NADH and the glucose absorbance measured and then the glucose concentration of the unknown sample calculated using spectrophotometer. The relationship between the absorbance and sample concentration was confirmed using Beer and Lambert’s law,after calculation of the experimental results.

Methods

Measured amount of water, enzyme and standard glucose were prepared for the experiment. An unknown specific amount of glucose was also included in the experiment. The standard glucose was added to water using six test tubes followed by the step two in which four test tubes were used for the unknown glucose with enzymes to catalyze the reaction in order to form an absorbent product.

In order to ensure complete performance of the experiment, cuvettes were also prepared and the spectrophotometer. Prior preparation was advocated so as to ensure smooth conduction of the experiment.

The experiment was conducted as follows. First, glucose and water were mixed together. The first test tube was used to put just 1.0ml of water. Subsequently, 0.8 ml of water were mixed with 0.2ml of glucose in another test tube and labeled test tube 2.

In the third test tube, 0.4ml of glucose was used with 0.6ml of water. The trend was continued with subsequent portions of glucose and water varying the glucose quantity with a constant amount of 0.2ml for every increase for water. The water variation was also done decreasingly with the constant amount. The changes in the amounts of the substances varied up to the sixth test tube that lacked water and had a glucose concentration of 1.0ml.

When preparation of the six test tubes, 100 μl was transferred to empty tubes one after the other. The amounts transferred from each sample were mixed gently and then later transferred for incubation for 15 minutes at normal temperature.

The unknown concentration samples were labeled A, B, C and D respectively. All the samples were put into other tubes with corresponding labels. Immediately after this step, 1.0ml of enzymes was added to each test tube before being incubated for 15 minutes at normal temperature.

All these samples prepared, were taken for incubation. After the amounts were taken from each test tube 1 to 6 and also A to B and placed in the cuvette for indirect reading via the spectrophotometer. The spectrophotometer was adjusted to a wavelength of 340nm which was taken as the ideal wavelength for measuring the NAD absorption. The spectrophotometer was calibrated through addition of the blank tube, after which all the samples were read individually.

Result

The obtained results were then recorded in a piece for the manipulation of the values obtained as below. A table was drawn to represent the value for easy comparison of the sample results that were obtained.

Table 1: Glucose with known concentration

The glucose concentrations increased steadily with a constant variation showing direct proportionality by 0.4mM according to this formula C2 = C1 x V1 / V2, where V2 equal 1ml, C1 2 mM and V2 values of glucose. Then, the glucose amount was obtained from the values of the standard glucose concentration using Beer-Lambert law, usually the formula written as Mass (g) = conc. (Mol/L) x vol (L) x Mol. weight (g/mol). This formula, where Mass refers to the Glucose amount, conc. representing the Glucose concentration of standard and vol is 0.001 L.

The spectrophotometer readings were recorded on the third column. The values obtained showed progressive increase with increase in quantity of the standard glucose, this direct proportionality is used to justify the Beer and Lambert’s law. Thus according to this law, the absorption of glucose, thickness of the absorbent and concentration of the samples are directly proportioned.

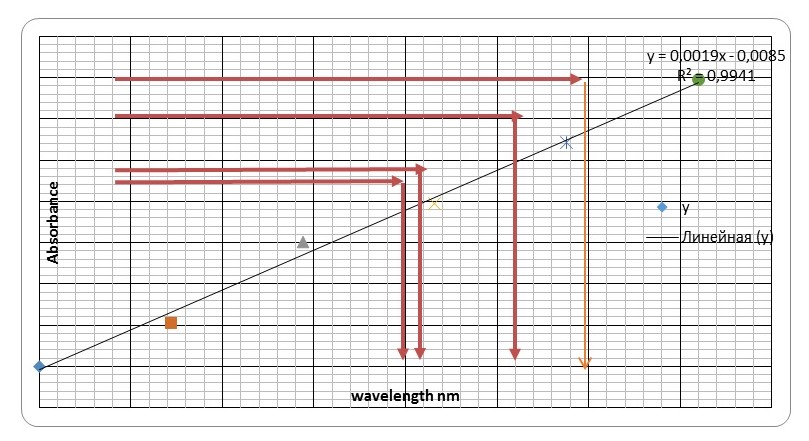
The results of the sample glucose with unknown concentrations were recorded in the second table. The calculations were done following the formula discussed later or alternately using Beer-Lambert law calculator. Therefore, glucose values were taken from the equation of the Figure 1 above (y = 0.0019x – 0.0085)… In this case the formula becomes x = y – c ÷ m, where y is Spectrophotometer reading. For example, (x = 0.427 – 0.0085 ÷ 0.0019) = 220.26 μg, as mentioned in the table below. In the last column the glucose concentration is taken by this formula (conc. mM = mass (μg) ÷ M. wt.), where mass is glucose amount and M. wt. is a constant value equal 180. As an example, (conc. mM = 220.26 ÷ 180 = 1.22 mM ).

Table 2: unknown glucose concentration

The results for the unknown glucose concentration were given as in the above table and it reflected the same proportionality originally seen with the standard glucose according to Beer and Lambert’s law.

Discussion

The application of Beer-Lambert law in this experiment surfaces a number of practical orientations that are necessary in general chemical analysis and particularly, biological sciences. The law is applied in the analysis of the unknown samples using spectrophotometer (Bonner & Hargreaves 2011, p. 237).

In the measurement and subsequent analysis using the spectrophotometer, the possible molar concentrations of both the known samples and unknown samples are calculated and incorporated in the equations. The values can be calculated as follows using the Beer and Lambert’s law as follows.

The particles concentration is represented in the slab by N. It then follows a fraction absorbed, photons, as they pass through the slab will be equal to the sum of the particles opaque area in slab. This is summarized by;

dl~= -αNI~dz.

It should be noted that since there are less protons passing through than on the slab, dl_z is negative ( it has a propositional magnitude with the protons number)

By integration of both sides of the function, we get a solution to the equation.

ln(I~) =-αN_z+ C.

the slabs intensity of thickness is l₀ at z=0. Applying the previous equation, the intensity difference is written as, ln(I_l) –ln (I₀)= (-αln+C)-(- α0N+C)= -αlN

Exponentiation and rearranging the yields A= -log₁₀ (I_l/I₀) =α’l/2.03=αl=∑ lc

For the Beer-Lambert’s law to hold certain prerequisites must be factored in the experiment, these are: the absorbers are expected to act independently of each other and the medium is also expected to be homogenous in the volume interaction and also the absorbing medium is expected not to scatter the absorbing medium.

Reference

Bonner, P., & Hargreaves, A., (2011) Basic Bioscience Laboratory Techniques: A Pocket Guide. Wiley.