Estimating expected returns is crucial for the investors, as it helps to make informed decisions. Expected returns help to anticipate the profit or loss from an investment in a situation of uncertainty (Magni, 2020). Investors can estimate returns from either one investment or a portfolio investment based on historical performance (Magni, 2020). Expected returns are calculated based on predictions for different scenarios in the development of a company. For instance, if we consider different economic condition as possible scenarios, expected return will be calculated using the following formula:
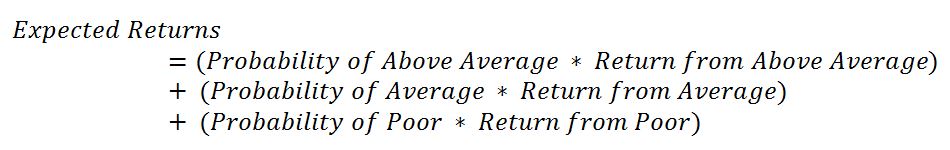
Apart from expected returns, investors also calculate the standard deviation of returns to determine the volatility of possible returns from investment. The standard deviation as a square root of the variance. The formula for variance is provided below
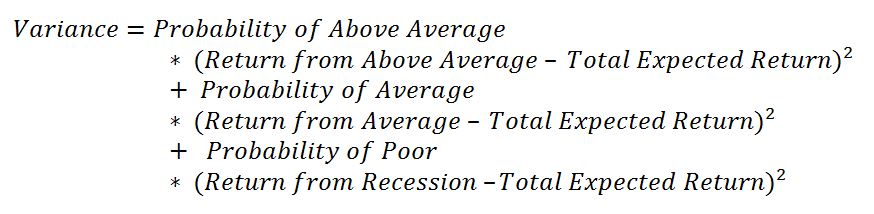
Assuming a scenario company faces a 20%t chance of a poor economy, a 40% chance of an average economy, and a 40% chance of an above-average economy with estimated returns of 10%, 18%, and 30% correspondingly, the expected returns can be calculated the following way:
![]()
Now, using the total estimated return, the standard deviation of the investment can be calculated:
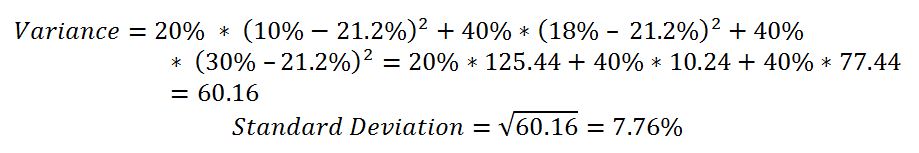
Thus, the calculations demonstrated that the expected return for the company was 21.2%, while the standard deviation was 7.76%.
Calculating standard deviation helps to determine risks of investment. In particular, the higher the standard deviation, the wider is the spread of possible returns, which implies higher uncertainty (Beers, 2022). In other words, the higher is the standard deviation, the higher are the risks of investment (Beers, 2022). Investors tend to have different tolerance to risk, which implies that calculating investment risks is crucial for all types of investors. While some investors can tolerate more risk with a chance of higher return, others have lower risk profiles, which implies that they prefer lower risks rather than having a chance at higher returns.
It should also be noted that standard deviation may depend upon numerous factors or condition. The example provided is a simplistic model that includes only three possible variations of one variable. However, there may be other variables that can affect expected returns, such as financial market conditions, market sentiment and expectations, interest rates and currency risks, labor costs, policies, regulations, and taxation (Magni, 2020). Portfolio managers take into consideration all the possible risks before making an investment.
References
Beers, Brian. (2022). How Is Standard Deviation Used to Determine Risk?
Magni, C. A. (2020). Investment Decisions and the Logic of Valuation: Linking Finance, Accounting, and Engineering. Springer International Publishing.