Introduction
Internal Combustion Engines (ICEs) have become the most common sources of power in most industrial processes. These engines are preferred due to their reliability and lack of complexity, and relatively low cost of operations (Okubo & Kuwahara 2020). However, despite these benefits, ICEs account for 15-18% of the global greenhouse gas emissions (Mejia et al 2020). In addition, the increased use of these machines in most applications will add to this pollution. Consequently, governments and international organizations have set strict standards to reduce emissions, and improve the efficiency of ICEs.
Enhancing efficiency of ICEs can be achieved by reducing fuel consumption. This enhancement requires the reduction of mechanical losses that reduce the engine’s power. The mechanical losses arise from friction, pumping system inefficiencies, and the movement of engine components (Ochoa, Isaza-Roldan, & Duarte 2020). In particular, friction accounts for up to 12% of the energy loses in the ICEs (Okubo & Kuwahara 2020). Most of this friction arises from the interactions between the piston skirt and cylinder liner, bearings, and the camshaft (Profito, Tomanik & Zachariadis, 2016; Ali et al 2016; Kirner et al. 2016; Liu et al. 2020). As a result, different studies have proposed methods for minimizing energy losses including heating the oil system (Forero, Ochoa, & Alvarado, 2020), applying low-viscosity oil (Duarte, Ochoa & Rojas 2020), smoothening the contact surfaces (Gropper, Wang & Harvey 2016; Mengi et al., 2020), and coating (Wang, et al 2020). Other alternatives include the optimizing the engine designs to minimize friction associated losses. However, lubrication remains the most common method of reducing friction between interacting planes in relative motion.
Aims and Objectives
This research explores the factors that influence the lubrication of valve train components. Firstly, it explores the effect of load on the lubricant film’s thickness when the engine speed is maintained at 400 revolutions per minute (rpm). Secondly, it explores the effect of rotational speed on the film thickness when the engine has a constant load of 10 kN. Thirdly, it explores the relationship between the film thickness and the Somerfeld’s equation. Lastly, it applies the Reynolds equation to evaluate the distribution of pressure in the oil and lubricant film thickness as a function of load and speed. These research questions will help in determining the optimal lubricant film thickness needed do minimize friction when the engine is subjected to various loads and speeds, and to minimize the engine’s wear and tear.
Literature Review
Recent demands on efficiency and strict omission standards have renewed focus on tribology. On the one hand, studies by Erdoğan, et al. (2020) propose the use of exhaust post-treatment systems including particle filters, use of catalytic converters, and catalytic reductions. While these post-combustion applications reduce emissions, they do not address the frictional losses arising from moving parts in the ICEs. In addition, the structure of most ICEs limits the application of these post-combustion filters, as their use increases back pressure in the exhaust system (Abril, Rojas, & Florez 2020). Further, such increase in pressure necessitate the addition of powerful pumps, which, in turn, increase the fuel consumption. For these reasons, recent studies focus on alternative strategies of boosting efficiency and reducing emissions.
Several studies find that reducing fuel consumption can achieve the dual objectives of reducing emissions and boosting efficiency. Firstly, Abril, Rojas, & Florez (2020) note that mechanical losses account for most of the energy losses in the ICEs. In addition, Knauder, et al. (2020) notes that friction accounts for up to 12% of the total energy lost in these engines. Consequently, studies recommend the use of the low viscosity oil, coating, and smooth contact surfaces to enhance efficiency (Tormos et al. 2017). Others propose the optimization of the engine designs to enhance efficiency (Consuegra et al. 2019). These studies indicate that effective lubrication and design optimization can reduce frictional losses and boost the efficiency of the engines.
Improving tribological performance between the compression rings and the cylinder liner enhances the engine’s efficiency. Recent studies find that lower frictional prolongs engine life, boosts engine efficiency, and reduces the emissions (Lu, Wood & Gee 2016; Turnbull et al. 2020; Menacer & Bouchetara 2020). In addition, enhancing the tribological performance boosts the braking power for vehicles, and reduces the consumption of lubricating oil, and lengthens the maintenance intervals (Forero, Ochoa, & Rojas, 2020). Forero et al. further point out that fuel consumption can be reduced by up to 1.5% by reducing mechanical friction. Consequently, tribology has significant implication for engine performance and emission reduction.
Lubrication reduce the contact between moving surfaces. Effective lubricants must maintain the moving surfaces separate under all temperature, speed, and load conditions (Goltsberg & Etsion 2016; Chen at al. 2020; Nouri, et al. 2019). In addition, they must remain adequately stable for them to remain effective over their useful life. Moreover, they must protect the surfaces from aggressive products that accumulate during operations. Finally, they should have the ability to clean the surface and hold dirt in order to collect the residue and debris that forms when in motion. The effectiveness of common lubricants is defined by their viscosity.
Viscosity refers to the flow characteristics of a liquid. Joysula et al (2021) note that as temperature increases, viscosity declines. Since ICEs run at high temperature, lubricants have to withstand the heat and remain effective in preventing friction even at high temperature. Chen at al. (2020) notes that viscosity influences the thickness of the film separating the metallic surfaces in relative motion. Studies by Singh, Gu, Fieldhouse, Singh and Singal (2014) find that lubricant viscosity does not have a significant effect on engine performance at low speed, but hinders performance at higher speed. Further, Singh et al. find that higher load induces power loss at a constant function of n0.75, where the n is the dynamic viscosity of the lubricant. Moreover, Singh et al. find that low lubricant viscosity results in low fuel consumption. Therefore, the engine lubricant rheology has a significant impact on the performance of ICEs.
Designers can optimize the tribological properties by adjusting the surface texture of the moving surfaces. Wang, et al. (2018) find that micro-texturing of the valve plate enhances the distribution of lubricants on the surface, thereby reducing friction. Adjusting the material’s crystallographic parameters and its micro-structure such as shape, crystal orientation, chemical composition, and relationships enhances the oil-film lubrication characteristics of valve plates (Knauder et al. 2020; Lu, Wood & Gee 2017; Gachot et al., 2017; Chong et al. 2019). Wang, et al. conclude that a fixed micro-texture radius causes an initial increase and subsequent decrease in the oil film’s frictional force, its carrying capacity, and load torque. They also find that small oil film thickness produces higher oil film pressure, thereby boosting the surface’s load bearing capacity. Since micro-texturing increases the film thickness, it reduces the frictional force, and reduces energy loses. They conclude that micro-hemispherical texturing and micro-cylindrical texturing offers the highest and second highest improvement in friction, whole micro-square texturing has the lowest improvement.
Studies use various models to determine the optimal speed application to result in lowest power loss. Panthi, et al (2015) use the Raimondi-Boyd’s model to determine the optimal film thickness with the help of the Reynolds equation. They generate a chart that display the change in oil film thickness in relation to changes in attitude angle, dynamic coefficients, and maximum pressure generated from the project. Other studies use phase change, ultrasonic amplitude, and resonant dip models to determine the circumferential film thickness profiles of a journal bearing (Beamish, Brunskill, Hunter, & Dwyer-Joyce, 2020). The application of more than one model allows for a comprehensive analysis of the oil film thickness for a wide range of shaft rotational angles.
Results
The first analysis explored the oil film thickness under different shift rotational angels. The shaft rotated at 400 revolutions per minute, and had a load of 20kN. The experiment used five models that included the resonant dip model, phase change model, amplitude model, Raimondi-Boyd-Maximum and Minimum model. Firstly, varying the shaft rotational angle from 0-750 ° shows a large, wave-like change in the Oil film thickness. The oil film thinned steadily from the 51.60µm at 0° to the lowest point at 100°. A further increase in shaft rotational angle results in an exponential increase in oil film thickness to a maximum of 93.27 µm at 300°. Additional increase in the shaft rotational angle lowers the oil film thickness before raising to a subsequent peak level at around 600°. Figure 1 shows the change in oil film thickness in response to a change in shaft rotation angle.
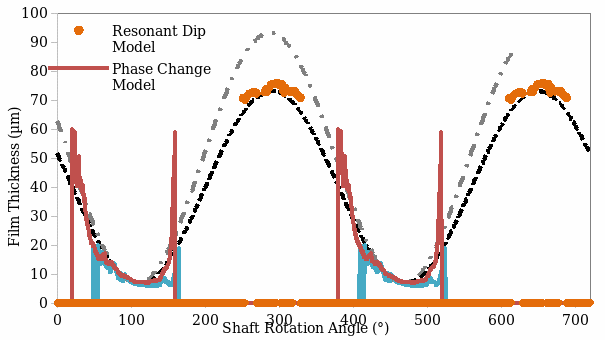
Figure 1 shows that the Raimondi-Boyd maximum and minimum models had the most comprehensive illustration of the change in oil film thickness for the range of shaft rotation angles. In contrast, the resonant dip model showed a few values clustered at the two peaks of the Raimodi-Boyd waves. Similarly, the amplitude model showed a constant reading of the oil film thickness when the shaft rotation angle exceeded 156°. Therefore, the resonant dip and amplitude models were less reliable in determining the exact point at which oil film thickness is highest.
The phase change model showed more responsiveness compared to the Amplitude model. Results from this model show a gradual decline in oil film thickness as the shaft rotation angle approaches 100°. The thickness stabilises before peaking at 159°. However, unlike the Raimondi-Boyd models that showed a smooth curve at the peak, the phase change model sowed a flat peak starting from 159-383°. In the same way, the model shows a right-angled trough after 383°, and does not show the effect of further increase in shaft rotation angle on the oil film thickness beyond 520°. Consequently, this model is not reliable in determining the exact shaft rational angles that result in the largest oil film thickness.
The second experiment used reflection coefficient to determine the change in oil film thickness as a result of changes in rotation angle of the shaft. The experiment calculated the reflection coefficient by comparing the relative amplitude of the measurement signal against a reference signal while varying the frequency (Beamish, Brunskill, Hunter, & Dwyer-Joyce, 2020). This experiment used a frequency range of 0-12 MHz, which offered an optimum noise to signal ratio. In addition, the experiment calculated the phase change by deducting the measurement and reference phases at each frequency. These values were mapped against the encoder data to determine the change in reflection coefficient and phase for each shaft rotation. Figure 2 shows the graph of change in reflection coefficient for a shaft at various rotational angles at 200rpm and with a load of 20kN.
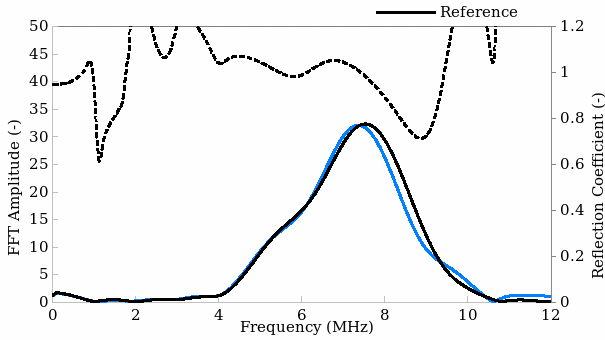
Figure 2 shows that the reflection coefficient increases at a frequency of 4MHz and peaks at about 7MHz. The reflection coefficient is affected by noise in as the FFT amplitude decreases, which means that the usable bandwidth for this test ranges from 5-7MHz. The highest reflection index is reached at a frequency of 7.5 MHz, which reflects the largest oil film thickness in the experiment.
The last experiment used the Sommerfeld number to compare the optimal film thickness of lubricant oil derived from the amplitude, phase, and Raimondi-Boyd models. The Sommerfeld number is a single parameter that guides the design of journal bearings, as large loads, low lubricant viscosity, or low angular speeds produce the same operating journal bearing eccentricity (Beamish et al 2020). The Sommerfeld number shows the bearing journal’s attitude angle and eccentricity that defines its performance as derivatives of lubricant viscosity, load, and operating speed. Figure 3 shows the comparison of the amplitude, phase, and Raimondi-Boyd models using the Somerfield number.
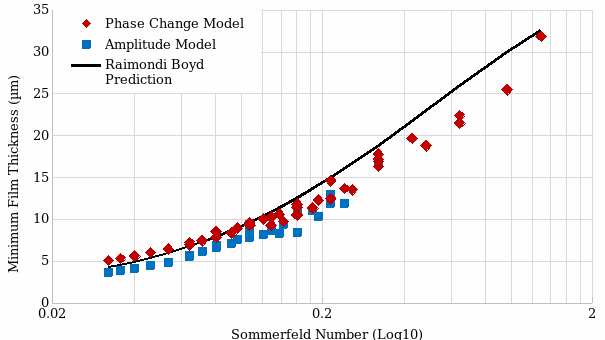
Figure 3 shows that results from the three models are closely clustered together with minimal deviation from the average value. The data points used an average of the minimum film thickness measurements for all cycles. Therefore, the three models are reliable estimators of minimum film thickness when expressed using the sommerfeld number.
The thickness of the lubricant film can be modelled using the Reyold’s equation. Reynolds equation is a differential function that governs the distribution in a Newtonian lubricant film (Habchi 2018). The equation assumes that oil has a negligible mass, has constant pressure, experiences no slip, is laminar, and has constant viscosity. In addition, it assumes that the lubricant film is Newtonian, and the inertial and surface tension forces are negligible when compared to the forces arising from viscosity. Lastly, velocity gradients and sheer stresses are meaningful across the film only as the film is extremely thin. If a film satisfies these assumptions, it can be modelled using the Reynolds equation.
Discussion
The valve train comprises of camshaft, bearings, and valve stem. These parts experience friction when the engine is in operation with the contact between the camshaft and follower having the largest contribution to energy losses through friction. Abril, Rojas and Florez (2020) note that the air and fuel intake stage of the internal combustion cycle suffers the highest energy losses due to the high energy exerted on roller by the lobe to force the valve to move. As a result, the oil film thickness declines during the intake stage to a minimum of 0.1µM. In contrast, the maximum friction force is realized during the combustion stage at the center of the piston. Westerfield et al. (2016) attributes this increase in friction to the greater interaction between cylinder liner and the rings. The frictional force varied based on the load and number of revolutions per minute.
The thickness of lubricating oil film can be used to determine the frictional force exerted on a radially interacting plane. This study demonstrates that angular variations, speed of rotation, and load have a direct influence on the circumferential film thickness of lubricants. The results showed that angular variations had the most significant impact on the film thickness. Consequently, designers can determine the optimal performance parameters to attain the largest film thickness needed to minimize friction and load.
The amplitude model produced the most comprehensive measurement of film thickness. Beamish et al (2020) note that the amplitude model can be used to measure films as thin as 0.2 µM. Since almost all bearings operate with films thicker than 0.2µM, the amplitude model offered a smoother and complete curve over the range of operating conditions. In contrast, the resonant dip model could not measure the film thickness for shaft rotation angles lesser than 243°, between 343-600° and exceeding 702°. While the model effectively determined the shaft rotation angle that led to the maximum film thickness, it does not reveal the thickness at a considerable range of angles. Therefore, the resonant dip model cannot be used to illustrate the minimum film thickness for shafts with a large variation of rotational angle.
The phase shift model uses reflections of ultrasonic pulse to determine the thickness of an oil film. Part of the pulse is transmitted while the other is reflected (David & Cheeke 2017). The proportion of reflected wave reflects the film thickness of the lubricating oil. In this study, the phase change model was used to determine the changes in film thickness arising from variations in the angles of shaft rotation. The results show the levelling of the maximum film thickness at areas that correspond to the other measurement methods. Therefore, the method shows a range of angles at which the film thickness offers the highest lubricating effect without distinguishing the exact points at which oil film offers the highest lubricating effect. For an infinitely thick layer, extrapolation can be used to determine the corresponding amplitude and phase, as the phase shifts reflect a near-perfect linear motion within a specified range.
The findings have three important implications for research and practice. Firstly, the shaft rotation angle has a significant impact on the film thickness, and the consequent effectiveness of the lubricant. Therefore, designers of internal combustion engines should adjust the angle of shaft rotation to realise the highest thickness of lubricating film, thereby reducing the energy losses incurred due to friction. Secondly, use of the Raimondi-Boyd model offers the best illustration of the changes in film thickness in response to the variation in angle of rotation of the speed. The model offers an exact angle point at which the film thickness is at its maximum. Each of the two peaks of the Raimondi-Boyd offers an optimal setting for an internal combustion engine. Thus, by varying the rotation angle of each shaft, one engine can be configured to carry different loads and still maintain the maximum effectiveness of the lubricant. Finally, since all engines must operate at varying speeds and loads, designers should use micro-texturing to boost the oil film thickness. Specifically, the micro-hemispherical texturing offers the highest and second highest improvement on the lubricating effect. This reduction in friction boosts the efficiency of the internal combustion engines, reduces their emissions, and extends their useful lives.
Conclusion
Reducing frictional losses during operation of Internal Combustion Engines (ICEs) holds the key to reducing emissions and minimizing their fuel consumption. These engines use oil to minimize contact between the moving parts. The thickness of the oil films between these moving parts determines the effectiveness of the lubricating effect of the liquid. However, the thickness depends on the speed and load exerted on the moving surfaces.
This research finds that varying the angular rotation of the rotating shafts changes the thickness of the oil film between the contact surfaces. Using the various methods, this study demonstrates that optimal lubricating effect is reached at various points of the angular motion. The corresponding peaks offer the least potential fuel consumption at the stated weight and speed. These peaks can be used as the optimal operating points for various loads and speeds of internal combustion engines.
One key limitation of this study is the lack of the lack of measurement of film thickness at low rotational speeds. If the shaft makes an incomplete rotation at very low speed, the film thickness cannot be measured accurately. Consequently, subsequent studies should use alternative methods of measuring film thickness such as installing ultrasonic transducers on the bearings. In addition, installation of a torque meter would facilitate additional analysis of the relationship between friction and oil film thickness. Nevertheless, the study offers a reliable method of determining the optimal conditions for minimizing friction.
Reference List
Abril, S.O., Rojas, J.P. & Florez, E.N. (2020). Numerical methodology for determining the energy losses in auxiliary systems and friction processes applied to low displacement diesel engines. Lubricants 2020, 8(12), 1-25.
Ali, M.A., Xianjun, H., Mai, L., Qingping, C., Turkson, R.F., & Bicheng, C. (2016). Improving the tribological characteristics of piston ring assembly in automotive engines using Al2O3 and TiO2 nanomaterials as nano-lubricant additives. Tribol. Int., 103, 540–554.
Beamish, S., Li, X., Brunskill, H., Hunter, A., & Dwyer-Joyce, R. (2020). Circumferential film thickness measurement in journal bearings via the ultrasonic technique. Tribology International, 148 (106295), 1-19.
Chen, Y., Jha, S., Raut, A., Zhang, W., & Liang, H. (2020). Performance characteristics of lubricants in electric and hybrid vehicles: A review of current and future needs. Frontiers in Mechanical Engineering, 6, 1-19.
Chen, Z., Goltsberg, R., & Etsion, I. (2017). A universal model for a frictionless elastic-plastic coated spherical normal contact with moderate to large coating thicknesses. Tribol. Int., 114, 485–493.
Chong, W.F., Hamdan, S.H., Wong, K.J., & Yusup, S. (2019). Modelling transitions in regimes of lubrication for rough surface contact. Lubricants, 7, 1-21.
Consuegra, F., Bula, A., Guillín, W., Sánchez, J., & Duarte, J. (2019). Instantaneous in-cylinder volume considering deformation and clearance due to lubricating film in reciprocating internal combustion engines. Energies, 12, 14-37.
David, J & Cheeke, N. (2017). Fundamentals and applications of ultrasonic waves. New York, NY: CRC Press.
Duarte, F.J., Ochoa, V.G., & Rojas, J. (2020) Effect of the geometric profile of top ring on the tribological characteristics of a low-displacement diesel engine. Lubricants, 8, 83-4.
Erdoğan, S., Balki, M.K., Aydın, S. & Sayın, C. (2020). Performance, emission and combustion characteristic assessment of biodiesels derived from beef bone marrow in a diesel generator. Energy, 207, 118-300.
Forero, J.D., Ochoa, G.V., & Alvarado, W.P. (2020) Study of the piston secondary movement on the tribological performance of a single cylinder low-displacement diesel engine. Lubricants, 8, 97-8.
Forero, J.D., Ochoa, G.V., & Rojas, J.P. (2020). Effect of the geometric profile of top ring on the tribological characteristics of a low-displacement diesel engine. Lubricants, 8(8), 83-84.
Gachot, C., Rosenkranz, A., Hsu, S.M., Costa, H.L. (2017). A critical assessment of surface texturing for friction and wear improvement. Wear, 372, 21–41.
Goltsberg, R., & Etsion, I. (2016) Contact area and maximum equivalent stress in elastic spherical contact with thin hard coating. Tribol. Int., 93, 289–296.
Gropper, D., Wang, L., & Harvey, T.J. (2016). Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int., 94, 509–529.
Joysula, S.K., Dube, A., Patro, D., & Veeregowda, D.H. (2021). On the fictitious grease lubrication performance in a four-ball tester.Lubricants, 9 (33), 1-11.
Kirner, C., Halbhuber, J., Uhlig, B., Oliva, A., Graf, S., & Wachtmeister, G. (2016). Experimental and simulative research advances in the piston assembly of an internal combustion engine. Tribol. Int., 99, 159–168.
Knauder, C., Allmaier, H., Sander, D.E., & Sams, T. (2020). Investigations of the friction losses of different engine concepts. Part 3: Friction reduction potentials and risk assessment at the sub-assembly level. Lubricants, 8, 39-51.
Liu, C., Lu, Y., Zhang, Y.-F., Li, S., & Müller, N. (2017). Numerical study on the lubrication performance of compression ring-cylinder liner system with spherical dimples. PLoS ONE, 12, e0181574.
Mejía, A., Leiva, M., Rincón-Montenegro, A., Gonzalez-Quiroga, A., & Duarte, J. (2020). Experimental assessment of emissions maps of a single-cylinder compression ignition engine powered by diesel and palm oil biodiesel-diesel fuel blends. Case Stud. Therm. Eng. 1, 100613
Menacer, B., & Bouchetara, M. (2020). The compression ring profile influence on hydrodynamic performance of the lubricant in diesel engine. Adv. Mech. Eng. 12, 16-81.
Mengi, Y., Xu, J., Jin, Z., Prakash, B., & Hu, Y. (2020). A review of recent advances in tribology. Friction, 8(2), 221–300.
Nouri, J.M., Vasilakos, L., Yan, Y., Vasilakos, C. (2019). Effect of viscosity and speed on oil cavitation development in a single piston-ring lubricant assembly effect of viscosity and speed on oil cavitation development in a single piston-ring lubricant assembly. Lubricants, 7(10), 1-15.
Okubo, M., & Kuwahara, T. (2020). New technologies for emission control in marine diesel engines. New York, NY: Elsevier.
Profito, F.J., Tomanik, E., & Zachariadis, D.C. (2016). Effect of cylinder liner wear on the mixed lubrication regime of TLOCRs. Tribol. Int., 93, 723–732.
Singh, D., Gu, F., Fieldhouse, J.D., Singh, N., & Singal, S.K. (2014). Prediction and analysis of engine friction power of a diesel engine influenced by engine speed, load, and lubricant viscosity. Advances in Tribology, 1, 1-10.
Tormos, B., Ramírez, L., Johansson, J., Björling, M., & Larsson, R. (2017). Fuel consumption and friction benefits of low viscosity engine oils for heavy duty applications. Tribol. Int., 110, 23–34
Turnbull, R., Dolatabadi, N., Rahmani, R., & Rahnejat, H. (2020). An assessment of gas power leakage and frictional losses from the top compression ring of internal combustion engines. Tribol. Int., 142, 105991.
Wang, Z., Hu, S., Zhang, H., Ju, H., Yang, J., & Liang. (2018). Effect of surface texturing parameters on the lubrication characteristics of an axial piston pump valve plate. Lubricants, 6(2), 49.
Westerfield, Z., Totaro, P., Kim, D., Tian, T. (2016). An experimental study of piston skirt roughness and profiles on piston friction using the floating liner engine. Warrendale, PA: SAE International.