Introduction
Finite Elements Analysis (FEA) also known as Finite Elements Method (FEM) is an approach to solve a physical problem by solving the Governing Differential Equations by converting the Governing Differential Equations into a set of Linear Equations over smaller domains or elements known as element level equilibrium equations. These element level governing equations are then assembled or combined to produce a set of equilibrium equations, known as global equilibrium equations. Then boundary conditions are then applied to solve the global set of equations to find out the primary field variable (deflection, rotation etc.). Subsequently, the element level equations are solved in what is known as post processing of the results to find out stress.
Dividing the entire domain into smaller domains or elements is known as pre processing. It is very important to divide the entire domain into suitable elements to find a solution, which is correct and converges fast. Important attributes of an element are morphology (linear, triangular, quadrilateral, tetrahedral, brick, prism etc. to name a few), number of nodes (this determines whether the element is linear or quadrilateral) and degree of freedom per node. Element selection should be proper to get correct and accurate results.
In the subsequent sections, the type of element suitable for different kind of problems is briefly discussed.
Different Type of Elements
Beam Element
This is suitable of a structure which is long in one dimension and relatively short laterally loaded in transverse direction. One can use two node linear element with two degrees of freedom (displacement and rotation) attached to each node. This element is shown in the figure below
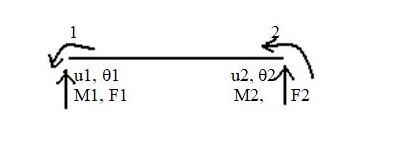
Shear Plate Element
To model a plate loaded in its plane, one needs to use a shear plate element. This is could be either a triangular or a rectangular element but each node will have five degrees of freedom u (displacement in x-direction), v (displacement in x-direction), w (displacement in z-direction), ux (rotation transverse to x-axis) and vy (rotation transverse to y-axis). These five degrees of freedom in case of a shear plate element are independent degrees of freedom unlike in case of bending pate element where u and v are related to rotation ux, vy and z.
Pressure Filled Plastic Bottle
To model a pressure filled plastic bottle one needs to use shell element. A shell can be seen as a thin plate with two curvatures. This element is a combination of Bending Plate Element and Shear Plate Element.
Fishing Rod
A fishing rod can be seen as two bars tied at a point. A bar can take only axial loading and can deform along axes only. However, when more than one bar is connected in a plane it forms a truss or frame. It can take not only linear loads but planer loads as well and the nodes now have two degrees of freedom. Therefore such an element is suitable for modelling a fishing rod. One should use a frame element or a two dimensional truss element. This is a two node linear element with two degrees of freedom (displacement along and transverse u and v) at each node.
A thick wall acting as flood protection barrier (Reddy, 2006).
This is can be modelled as thin plate element will small deflection. One can use different kind of plate bending elements like nonconforming triangular element, nonconforming rectangular element, conforming triangular element or nonconforming rectangular plate element. In case of nonconforming elements there are three degrees of freedom per node – these are deflection w and rotations ∂w/∂x and ∂w/∂y. However, these elements cannot ensure continuity of normal rotation at the line between the adjacent elements. However the error is not much and therefore people use nonconforming elements despite the problem of non-continuity of normal rotation at the adjacent edge. One can make a nonconforming element as a conforming element by adding another degree of freedom ∂²w/∂x∂y . This ensures continuity of the normal rotation at the edge between adjacent elements.
Shell Element
To model a water pump casing one needs to use shell element. A shell can be seen as a thin plate with two curvatures. This element is a combination of Bending Plate Element and Shear Plate Element.
Conclusion
From the discussion in the preceding sections one can see that different kinds of elements are needed to solve different kind of problem. The essence of selecting an element is that it should be able to incorporate all the primary field variables and should give a result which converges quickly towards the exact solution.
References
Reddy J. N. “An Introduction to The Finite Element Method”. 3rd Ed. 2006, Tata McGrow Hill, New York