From the literature, I understand that Ross, Westerfield and Jaffe (2013) support the need to study the merits and demerits of using the dividend growth model to estimate the stock price of a dividend and non-dividend-paying stock. Small and large firms have many growth opportunities, which can use the dividend growth model, which consists of the Gordon and Divide (GDM) and Discount Models (DDM) to calculate the stock prices.
I understand that DDM uses the actual terminal values to calculate dividends and GGM uses the annual company growth rate of dividends to calculate the stock price (Ayers, Cloyd & Robinson, 2002). Forecasting techniques are used to calculate the average growth rate of the stock price. The growth rate cannot exceed the IRR. The models cannot be used to predict the actual company earnings and growth rates (Ayers, Cloyd & Robinson, 2002).
How the variables affect the valuation of dividend and non-dividend paying stocks.
For the no-dividend paying stock, the dividend growth model uses variables of time, size, and the uncertainty of the flow of cash generated by stock to determine the price of the stock. Dividends define the cash flow of equities and can be used to determine the timing and growth of a firm (Ross, Westerfield & Jaffe, 2013).
Academicians and practitioners have proposed different types of models for calculating the cost of equity of the dividend and non-dividend paying stocks (Foerster & Sapp, 2005). An example of a company that holds dividend-paying stock is the NASDAQ operations. The dividend growth model provides a theoretical framework for calculating the prices of stocks, which have a zero growth rate as shown below.
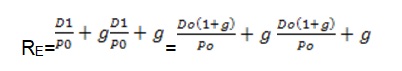
In the above model, RE is the required return on equity, P0 is the share’s current market value (%), DO is the dividend that has been paid, and g is the expected dividend growth (%) rate (Foerster & Sapp, 2005). The cost of equity provides information about the IRR, which can be calculated using historical data. If a person pays $ 10,000 the cost of equity is 6% of the dividend issuing company. The stock price can be estimated using the following method:
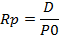
The discount growth model is appropriate for companies, which have grown and no longer need the cash from equity shareholders to conduct business transactions. The growth rate determines the price of the dividends. Middle-income companies pay 1% to 3% of the value of their shares and mature companies pay higher dividends.
One example of the non-dividend-paying stock is the Bank of Montreal. The company uses the dividend discount model (DDM) to calculate the value of the stocks’ Net Present Value (NPV). The similarity between the models is that the models use time as a factor to determine the price and value of the stock. I know the difference to be in the approach of the principle of reinvestment those models use to determine the stock prices (Foerster & Sapp, 2005).
References
Ayers, B. C., Cloyd, C. B., & Robinson, J. R. (2002). The effect of shareholder-level dividend taxes on stock prices: Evidence from the Revenue Reconciliation Act of 1993. The Accounting Review, 77(4), 933-947.
Foerster, S. R., & Sapp, S.G (2005).The Dividend Discount IVIodel in the Long-Run: A Clinical Study, Journal of Applied Finance, 53(12)pp. 55-75.
Ross, S. A., Westerfield, R. W., & Jaffe, J. (2013). Corporate finance (10th ed.). New York: McGraw-Hill Irwin.