Introduction
The provision of higher education in a country is affected by a number of factors including population, rural and urban population distribution, enrollment trends, gender, and ethnic background, etc. It is the responsibility of the Federal and State governments to ensure that there is sufficient number of colleges and universities to fulfill the educational needs of the population. There are various datasets published by National Center for Education Statistics, US Census Bureau, and US Department of Education, which can be analyzed to identify the key trends and relationships between different variables to understand the education status of the country. In this study, the demand and supply of higher education in the US is analyzed by conducting a parametric test.
The model considers the supply of higher education as the dependent variable and the demand for higher education as the independent variable. The supply of higher education (S) is determined by the number of higher education institutes in the US (National Center for Education Statistics (NCES), 2018a), and its data is collected from Statista. The demand for higher education (D) is determined by the number of undergraduate enrollment in the US (National Center for Education Statistics (NCES), 2018b). The relationship between demand and supply of higher education is based on the basic economic principle which states that the supply of a product or service is derived from the demand for it. A control variable is also added to the model is Cost (C), which represents the “average cost for tuition and other fees* at universities in the United States” (Institute for College Access & Success, 2018). The reason for adding the cost variable is that both demand and supply of higher education like any other service is affected by the tuition fee and other expenses incurred by students. Therefore, it could help in improving the model’s results.
The current research is a longitudinal study of the relationship between dependent and independent variables. In total, 15 values of each variable are collected from 1980 to 2016. The reason for this limited sample size is the inability of the researcher to find comparative data for all variables in the same period. The impact of the limited size sample on research outcomes would be assessed in the conclusion part of this report.
(I) The estimation of the relationship between dependent and independent/control variables is made by implementing a multivariate regression model that generates a linear equation in the following manner.
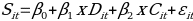
Where
Sit =Number of Higher Education Institutes
Dit =Total Enrollment
Cit =Average Cost for Tuition Fees
The multivariate regression model assists in determining the changes in the values of the dependent variable caused by the changes in the values of explanatory/independent variables (Keith, 2015). The strength and direction of the coefficient of the slope, βn is assessed for predicting the relationship between the selected variables. In the equation (I), εit represents the error or residual of the model, which is the value of the dependent variable not entirely predicted by the regression analysis.
Regression Analysis
The results of the multivariate regression model are given in Table 1.1-1.2.
Adjusted R2
The adjusted R2 is 0.8985. It indicates that approximately 89.85% of the variation in the number of higher education institutions (S) is explained by two independent variables— Total Enrollment (D) and Average Cost for Tuition and Fees (C).
Evaluation of Independent Variables Using a t-test
Table 2 provides the results of the t-tests for each of the independent variables.
Analysis of t statistics
Total Enrollment:
H0: βTotal Enrollment = 0; HA; β Total Enrollment β0
Reject H0 at the 5% level (P-value < 0.05)
Average cost for tuition and fees
H0: β Average Cost for Tuition and Fees = 0; HA; β Average Cost for Tuition and Fees β0
Do not reject H0 at the 5% level (P-value > 0.05)
Analysis of F
H0: βTotal Enrollment = βAverage Cost for Tuition and Fees = 0;
HA: at least one β is not equal to zero
F = 62.973
Critical value of F:
F(2,12) = 3.89
Since 59.5515 > 3.89, reject the null hypothesis. At least one of the β’s is not equal to zero.
Conclusion and General Comments
It could be concluded that the regression model implemented in this report has a high goodness of fit based on the value of adjusted R2. It is crucial for a model to have a high value of adjusted R2 as it implies that the relationship based on its results can be used for predicting changes in the value of the dependent variable. Although the current model used only two independent variables and 15 data observations, the higher value of adjusted R2 means the model is robust, and it can be used in the real-life setting.
(II) The following regression equation is obtained from the values of coefficients given in Table 2.
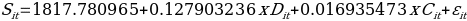
The coefficient of the slope of Total Enrollment (Dit) has a higher value than that of Average Cost for Tuition and Fees (Cit). The research outcomes also indicate that there is a positive influence of Total Enrollment and Average Cost for Tuition and Fees. It implies that when the population grows and the number of individuals seeking higher education increases, the number of colleges and universities also increase. Furthermore, the positive relationship between cost (price) and supply implies that when the cost (price) goes up, the supply of higher education also increases. Since the level of confidence assumed for testing the results of the regression model is 95%, therefore the p-value is compared with the standard error term of 5%. The relationship between Supply and Total Enrollment is found to be significant since its p-value is less than 0.05. On the other hand, the relationship between Supply and Average Cost is found to be insignificant since its p-value is more than 0.05.
Although the current analysis is performed by using real-life data, there are many other instances in my personal life in which regression analysis can help to predict the relationship between different variables. Every decision, which can be measured in numerical terms, can be assessed by using the regression analysis. However, it must be understood that not every situation or model is linear, and there are other types of regression techniques that can be used to predict relationships. One real-life example is the determination of my month saving, which is affected by various factors including income and expenses. My monthly income includes work related pay that I receive from my employer and the money sent to me by my parents. My expenses include food, travel, leisure, and others. The regression model can be implemented in which my monthly saving is the dependent variable, and my income and expenses are independent variables. Furthermore, my monthly saving is affected when I am staying at my parents’ house. Therefore, a dummy variable could be added to the model representing the time when I am at the college residence (0) or when I am at my parents’ house (1).
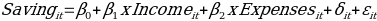
It is just one example, and there can be many decisions that could be analyzed by using the regression analysis. The model implemented in this report can be changed in the future given the assumptions made for the study are changed. It means that if the confidence level for testing the results is adjusted, then it could affect the significance of each variable. Furthermore, it is suggested that the value of adjusted R2 can be improved by increasing the sample size or by adding more explanatory variables in the model.
References
Institute for College Access & Success. (2018). Average cost for tuition and other fees* at universities in the United States from 2000/01 to 2013/14 (in U.S. dollars). Web.
Keith, T. Z. (2015). Multiple regression and beyond: An introduction to multiple regression and structural equation modelling (2nd ed.). New York, NY: Routledge.
National Center for Education Statistics (NCES). (2018a). Number of higher education institutions in the United States from 1980 to 2015. Web.
National Center for Education Statistics (NCES). (2018b). Undergraduate enrollment numbers in the United States from 1970 to 2027, by full/part-time attendance (in 1,000). Web.