The historical and practical significance of differential equations cannot be overstated. Centuries of research conducted by hundreds of mathematicians, physicists, economists, chemists and other scientists around the world have broadened the range of applications and solutions. For a better understanding of the thought processes behind those equations, there is a need to dive deep into the history of their creation and use.
Differential Equations
The differential equation as statements of equality that incorporate functions and its derivatives were first proposed by Isaac Newton and Gottfried Leibniz. Such equations emerged from the field of mechanics where there was a necessity to calculate coordinates of physical objects, their speed, and acceleration viewed as time functions under different conditions. Certain geometry questions were also reduced to differential equations. The term itself was developed by Leibniz in 1676 (Simmons 11). In the 18th century, Euler and Lagrange made a huge impact on the theory of differential equations. Euler, for instance, was the person who invented the notion of function and was the one who introduced the form of writing function and argument as f(x) meaning that function f is applied to argument x. He also introduced the presently widespread symbol ∑ for the sum. He synthesized the works of Newton and Leibniz to create tools such as the numerical approximation of integrals and Euler–Mascheroni constant that substantially simplified the use of their calculus in physics (Simmons 65). He also developed famous quasilinear hyperbolic equations for fluid dynamics that were later named after him.
Lagrange perfected the method of solving differentials called a variation of parameters that was originally discovered by Euler by applying it to the planetary motion. He varied the constants of the unperturbed motions instead of coefficients as proposed by Euler. By writing a series of works devoted to analytical geometry and other questions, Lagrange created grounds for the theory of partial differential equations, which were later published in collaboration with Euler.
Bernoulli was another scientist who contributed enormously to the theory and application of the equations. He was the first to apply the principle of variable separation that was later properly studied and rediscovered as Fourier method. Together with Euler, Bernoulli produced a simplified elasticity theory known as the beam theory that is currently central to structural and mechanical engineering. The scientist first used integrals and solved the equation that was later called Bernoulli equation (see fig. 1).
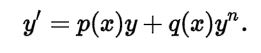
n here is a real number not equal to 0 or 1.
Jacopo Riccati was the person who contributed to further development of Bernoulli equation as an ordinary quadratic equation in the unknown function. After meeting Bernoulli in person, Riccati was troubled with a question of applying separation to variables in differential equations (Bittanti et al. 6). Together with his followers, Riccati was able to produce a new formula of a non-linear equation that was possible to reduce to second order linear ordinary differential equations (Kucera 154). The equation is as follows:
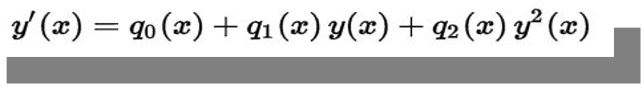
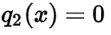
If then it was possible to reduce the equation to the standard Bernoulli equation of the first order.
In the 19th century, scientists were occupied by the problem of integration in quadratic equations. Lie was the person who contributed to the establishment of the theory of diffeomorphisms or as they were named “Groups of Lie.” They now represent one of the most fertile grounds for research in modern mathematics and algebra. However, the range of questions researched in this field is far from differential equations despite their large impact on the formation of Lie Groups.
The new stage of development in the sphere of differentials began from works of Henri Poincare, who created a qualitative theory of differential equations that explained that even if the equation cannot be solved through functions, a lot of data can be gathered from the form of the equation (Hale and Sjoerd 17). This theory together with complex variables formed the basis of modern topology. Poincare’s qualitative theory also developed into the theory of dynamical system, which is also a prominent area of research.
Application
Differential equations either formed the basis or helped establish the laws of many applied and theoretical fields of study such as mechanics, topography, physics, electrodynamics, quantum mechanics and other sciences (Simmons 21). In all of them, they helped solve toughest problems and explain various processes. In physics, for instance, the diffusion equation described the relation of particle concentration, spatial coordinates and time. The equation helps understand and control the movement of particles in solid materials when they are heated, which enhanced the quality of their fabrication.
Another example is the wave equation, which is a typical second order linear partial differential equation that explains the behavior of sound, water, and light waves in acoustics, fluid, and electromagnetics respectively. The heat equation (parabolic partial differential equation) explains the mechanics of heat spreading within the defined area and the time needed for the process to unfold.
Conclusion
All things considered, the differential equation is a complex and at the same time a crucial subject that is immensely influential in many areas where precise calculations are of the essence. Hundreds of famous scientists such as Newton, Leibniz, Euler, Bernoulli, Riccati, Poincare, Lie, and many others have contributed to finding new solutions and adapting them for applied fields of study. Thanks to their honored labor modern generation can construct rockets, advanced materials, create interactive maps and many other things.
Works Cited
Bittanti, Sergio, et al. The Riccati Equation. Springer Science & Business Media, 2012.
Hale, Jack K., and Sjoerd M. Verduyn Lunel. Introduction to Functional Differential Equations. Springer Science & Business Media, 2013.
Kucera, V. “From Differential to Algebraic Riccati Equations: The Influence of Kalman. Historical Perspectives.” IEEE Control Systems, vol. 37, no. 2, 2017, pp. 153–156.
Simmons, George F. Differential Equations with Applications and Historical Notes, Third Edition. CRC Press, 2016.