In the mathematical sciences, much attention is paid to classification and methods of solving equations: linear, quadratic, and polynomial. There is no doubt that the practical application of the equations can be found in any environment of public life: from sociology to rocket science. Thus, the precise identification of the type of equation and, what follows from it, the search for methods of solution is of paramount importance. In this paper, three types of mathematical equations will be discussed, and the methods for their solution will be investigated and compared.
Basically, all mathematical equations differ from each other by the highest exponent of the principal term. If one considers the writing of the equations as a polynomial, one must admit that for linear models, the highest exponent is equal to one, for square models, to two, and all other values are classified as polynomial equations (Eq. 1). Therefore, linear equations are those algebraic equations in which the full exponent of its constituent polynomials is equal to one (Eq. 2) (“Difference between linear & quadratic equations,” 2020). Quadratic equations are those in which a variable is elevated to a second power (Eq. 3). It should be understood that a quadratic equation can be complete — if all terms of the trinomial are present — and incomplete. Finally, a polynomial equation is any mathematical notion in which a polynomial with an exponent above or equal to three is equated to any number or other polynomial (Eq. 4). Thus, given the mathematical relationship of the equations described, it must be recognized that some of their solutions may be common. For specifics, Eqs. 5–7 show the designed formulas of the equations to be solved.
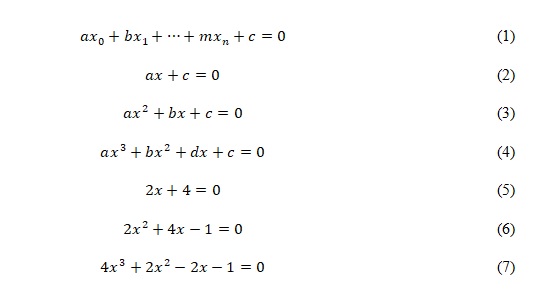
The geometrical method for solving almost any equation is to plot the function on the coordinate plane. By properties of the function, the intersection points of the graph — be it a straight line, a parabola, or a curve — with the x-axis are solutions. Therefore, if one takes some test points for each of the equations and apply them to the plane, one will find the roots shown in Figure 1. Although this method allows visualizing a solution and is suitable for all types of equations at once, one has to admit that the search for exact solutions can be complicated by non-integer values.
The second method, which can be applied to all models, but is also not strict, is the selection of values. In particular, in Eqs. 5-7, it would be possible to select at least one of the roots so that equality has a mathematical meaning. For example, the apparent answer to Eq. 5 seems to be the number -2, which turns the left side of the equation to zero. One must admit that selection is one of the working methods of searching for roots for polynomial expressions.
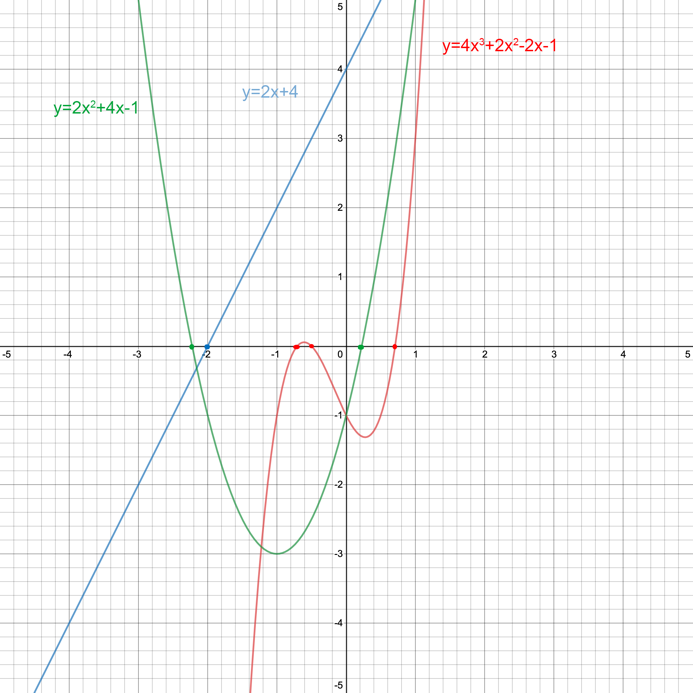
Linear equations are traditionally solved by moving the variable to the left side and numbers to the right side. Thus, Eq. 5 can be transformed into Eq. 8, which after division gives root x = -2 (“First-degree equations,” 2017). To solve a quadratic equation, the discriminant definition and root search formulas, as shown in Eq. 9, are usually used. Moreover, such equations may have two roots, one or none at all, which depends on the discriminant sign. At the same time, Vieta’s rules can be used for the solution. Moreover, polynomials of even exponents are traditionally reduced to square equations by replacing the highest power of the term so that it becomes square, as shown in Eq. 10. If binomials and polynomials can be factorized into a bracketed product, it means that such equations can be reduced to several lower-power equations: Eq. 7 can be factorized, as shown in Eq. 11.
References
Difference between linear & quadratic equations. (2020). Quadratic Equation. Web.
First-degree equations and inequalities. (2017). Quick Math. Web.