Summary
The hypothesis test study selected to help work on the conclusion is the Z-test. Z-test is a widely used hypothesis testing method that evaluates and determines whether or not an association or a finding is statistically significant (Dziak et al., 2020). A z-test examines the mean of a distribution and compares it to the expected value. To calculate the z-score, a researcher subtracts the mean from the raw score and then divides the result by the standard deviation. The main assumption when calculating the z-score is that the data is normally distributed (Illowsky, & Dean, 2018). The test can only be performed for a population greater than 30. The central limit theorem underscores the assumption because it is likely to be normally distributed as a sample size gets larger.
Example Scenario
When a business person wishes to know whether the daily returns on stock are above 1%, the z-test is paramount. The test can be calculated using a sample of 30 entries of daily recovery. If the sample is calculated and is found to have an average mean of 2%, and assuming that the standard deviation is 2.5%, then the claim that the mean is great than one percent is justified by calculation when the alpha value is 0.05.
Variables for Testing and the Guess
In the case of the businessman, the important variable under test is the population means and whether its value is higher than 1.5%. The guess set at the beginning of the test is that the mean is 1.5%. Based on the guess, the null and alternative hypotheses are given as H0: z = 1.5% H1: z > 1.5%, respectively. Given the condition, the z-score will be computed as:
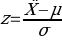
Where:
- ẍ a value from the population is,
- μ is the population mean, and
- σ is the standard deviation for the population.
z = 0.02-0.01 / 0.025
z = 0.4
The critical value can be obtained from the z-table by looking up from the left side of the column at 0.4 and checking the corresponding value, 0.65542. The corresponding value is then used to decide whether the variables are statistically significant (Dwijayanti et al., 202). The decision rule, in this case, is that the null hypothesis is rejected when z is greater than the critical value. In the case of the businessman, the null hypothesis is accepted because the available evidence refutes the claim that the mean is greater than 1.5%.
References
Dwijayanti, I., Nugroho, A. A., & Pratiwi, Y. I. (2020). Meta-analysis: Effect of problem approach and inquiry approach toward students’ mathematical critical thinking skill over the past 4 years. Al-Jabar: Jurnal Pendidikan Matematika, 11(1), 1-10.
Dziak, J. J., Dierker, L. C., & Abar, B. (2020). The interpretation of statistical power after the data have been gathered. Current Psychology, 39(3), 870-877. Web.
Illowsky, B., & Dean, S. (2018). Introductory Business Statistics. Web.