Introduction
About this research project, I would be interested in examining differences in international tourism between France and England. Specifically, this report highlights variations in the number of tourists in 5 years, i.e., 2009-2013. The secondary data that are used in calculations and conclusions were obtained via the following link.
It is pertinent to note that this paper has the following sections.
Section One – The Processing of Data
Various measures that are founded on statistics will be used to analyse facts. The following would be calculated: averages, interquartile ranges, and standard deviations.
Section Two – Displaying of Data
Many graphical methods will be utilised to represent information, such as tables, pie charts, pie charts, and bar charts.
Section Three – Analysis of Data
A discussion will be offered in terms of what the information from the data would show.
Section Four – A Critique and/Discussion of the Data
Critical analysis of the relevance of the data and impacts of extraneous data variables will be made.
Section Five – Own Idea for the Data Collection
In this section, opinions about the formulation of the research question in the future will be given.
Section Six – Evaluation of Own Ideas for Data Collection
This part will have ideas that would concentrate on what would be done to assess the secondary data in a better manner in the future.
Conclusion
The validity, reliability, and generalisation of the data used in the analysis will be provided.
Section One – Processing of the Data
I have calculated the average number of international visitors using the following formula:
Mean = sum of visitors divided by the number of years (5 years). I have also calculated standard deviations of the data based on the allowed variations that are within a 95% confidence interval.
Figure 1. A table showing the mean number of tourists who visited England and France in the 2009-2013 period. The table also shows standard deviation values for the computed data.
It is also important to calculate the extent to which the data are spread and determine the aspects described below:
- Maximum score – this is the highest value of a variable.
- Minimum score – this is the lowest value of a variable.
- Range – is the variation between the highest and lowest values (Green & Salkind 2010).
- Median – is defined as the value that lies in the middle of numerical figures that are arranged in ascending order (Pagano 2012). Because the sample size in this context is 5, the middle value is achieved by dividing five by 2 and adding 1.
- Lower quartile – this is obtained using the expression ¼(n + 1), where n is the sample size (Pagano 2012).
- Upper quartile – is calculated using expression ¾(n + 1).
- Interquartile range – this represents the extent to which upper and lower quartiles vary (Pagano 2012; Stevens 2013).
Figure 2. A table showing the results of various aspects of the spread of the numbers of tourists.
Section Two – Displaying of Data

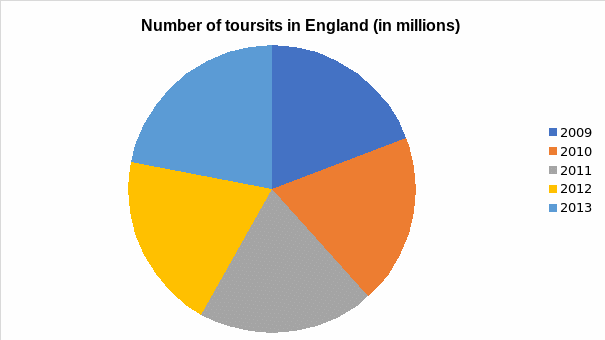
Pie charts are used to show the amount of a circle that is occupied by the various numbers of tourists concerning the five years. It is critical to note that the angle of the segment is determined using the following expression:
Angle of segment = (subtotal/total) x 360
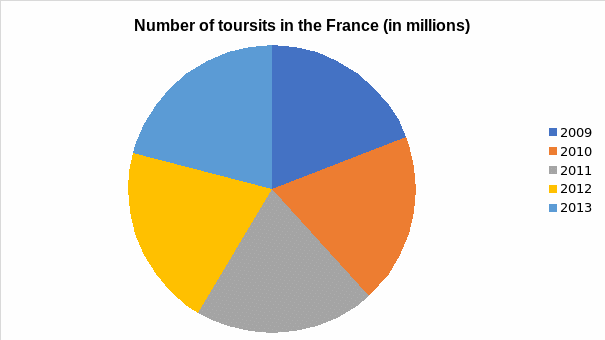
Section Three – Analysis of Data
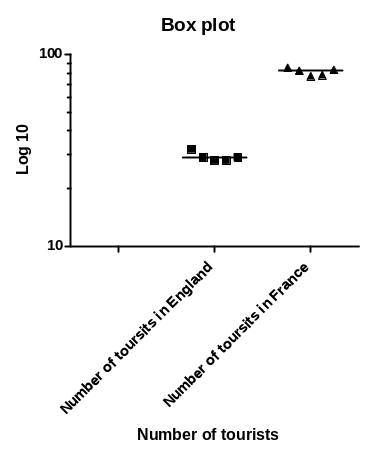
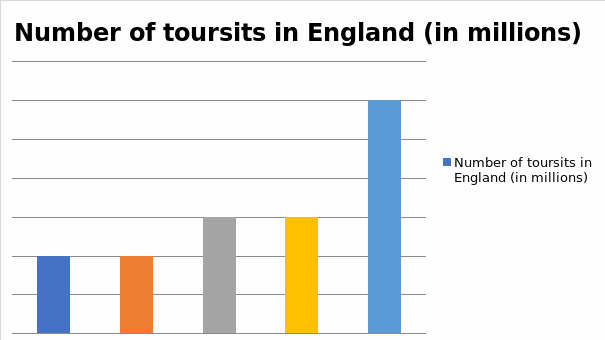
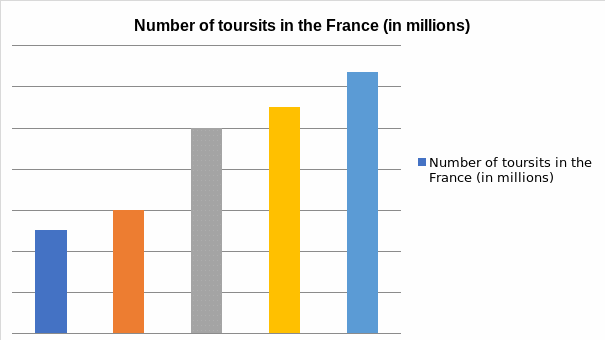
Figure 1 shows that France has more tourists than England in the five-year period that is analysed in this report, i.e., 29.2 million in England versus 81 million in France. However, as noted in figure 1, the data used in the analysis of France have more variability. Figure 2 exhibits that all statistical parameters in the analysis lie within the 95% confidence interval. The two box plots indicate that the number of visitors in the two nations does not maintain certain patterns. However, it is crucial to underscore that, as depicted in figure 5 and figure 6, the numbers of visitors in England and France have been increasing over the years. This could be due to the adoption of better tourist promotion approaches (Cooper, 2006; Höpken et al. 2010). The constant increases are also shown in the pie charts (figure 7 and figure 8).
Section Four – A Critique/Discussion of the Data
Although the secondary data were obtained from online databases, the persons involved in collecting them, and the initial sample sizes adopted could not be established. In addition, they did not include important information about age, marital status, income, and gender of visitors, yet they greatly impact tourist numbers (Ashworth & Larkham 2013; Boniface 2013).
Section Five – Own Idea for Data Collection
My secondary data did not analyse income about the frequency of tourists. A vital prediction is that richer people are more likely to travel to tourist attraction centres than poor persons (Cooper 2006). It would be important to conduct a retrogressive study that would focus on understanding relationships between tourist numbers and other aspects such as marital status and age.
Section Six – Evaluation of Own Ideas for Data Collection
Research shows that data have different degrees of variability. For example, a focus on income would be appropriate in one context, but inappropriate in another where ages of tourists would be important. Stratified sampling methods would be applied to avoid bias.
Conclusion
Based on the fact that statistical calculations were done perfectly, it would be concluded that the secondary data were valid, reliable, and accurate. However, they could have been improved by performing more tests and incorporating more variables. My idea for data collection could enhance the study by ensuring that data are handled in a better manner that would lead to a significant reduction in bias.
References
Ashworth, G, & Larkham, P, Eds, 2013, Building A New Heritage (RLE Tourism). Routledge, London, United Kingdom.
Boniface, P, 2013, Managing quality cultural tourism, Routledge, London, United Kingdom.
Cooper, C, 2006, ‘Knowledge management and tourism’, Annals of tourism research, vol. 33, no. 1, pp. 47-64.
Green, SB, & Salkind, NJ, 2010, Using SPSS for Windows and Macintosh: Analyzing and understanding data, Prentice Hall Press, Upper Saddle River, NJ.
Höpken, W, Fuchs, M, Zanker, M, & Beer, T, 2010, ‘Context-based adaptation of mobile applications in tourism’, Information Technology & Tourism, vol. 12, no. 2, pp. 175-195.
Pagano, R, 2012, Understanding statistics in the behavioral sciences, Cengage Learning, Boston, MA.
Stevens, JP, 2013, Intermediate statistics: A modern approach. Routledge Academic, London, United Kingdom.