Introduction
To understand arguments in mathematics, it is of necessity to comprehend how known facts are combined, to be capable of proving new facts. In logic, a statement refers to a sentence that can be categorized as being false or true, but with no vagueness (Royden, 2001). Truth value refers to the falsity or actuality of a logical statement. Conversely, The Venn Diagram is often employed in mathematics to display correlations between sets. It is composed of 2 or more circles that are overlapping (Bluman, 2005). This paper aims at employing Venn Diagrams to get the validity of the arguments below:

Validity of Arguments by use of Venn Diagrams
Typically, logical statements, which have fundamental connectives as well as negation, are correlated with those statements that have complements, connections, and unions, in the following manner: Let p be an object belonging to a set P, and q be an object belonging to a set Q. From that: “p ∧ q is equivalent to P ∩ Q; p ∨ q is equivalent to P ∪ Q; p →q is equivalent to P ∪ Q; and ∼p is equivalent to P” (Bluman, 2005, p. 23). In arithmetical arguments, the conclusions, as well as the premises/propositions, can be transformed into equivalent set statements, and from these statements, we can draw Venn Diagrams. For instance, if the Venn diagram (that is, for the Conclusion) is a subset of the premises intersection then the argument will be valid (Bluman, 2005).
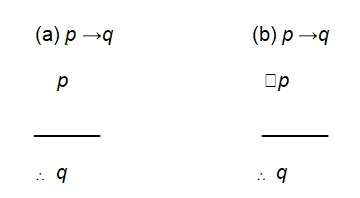
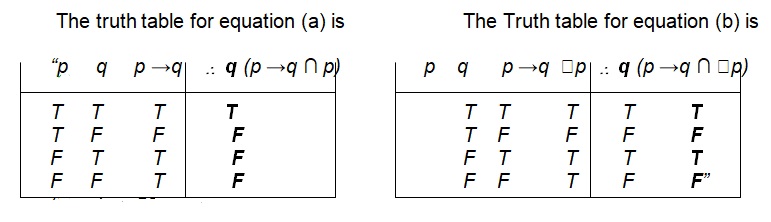
(Royden, 2001, p. 5).In equation (a) above, because the conclusions are rendered from the propositions, the set-statements in the conclusion are not equivalent to those in the premises. That is, ∴ q and q are not the same. Therefore, this argument is a fallacy. Conversely, in equation (b) above, the premises are translated into the conclusions and the set statements in the conclusion are equivalent to those in the premises. That is, ∴ q is equivalent to q. Therefore, this argument is not a fallacy.
An argument comprises propositions (premises) that results in a conclusion. To test an argument’s validity, both the propositions and the conclusions ought to be analyzed. Ideally, a mathematical argument is based on the assumption that the proposition is normally true. Idyllically, it is not the concern of logic as to whether the premises are true or false, but with the validity that can be deduced from them (Royden, 2001).
From the statements above, the Venn Diagrams of equations (a) and equation (b) are as shown below;
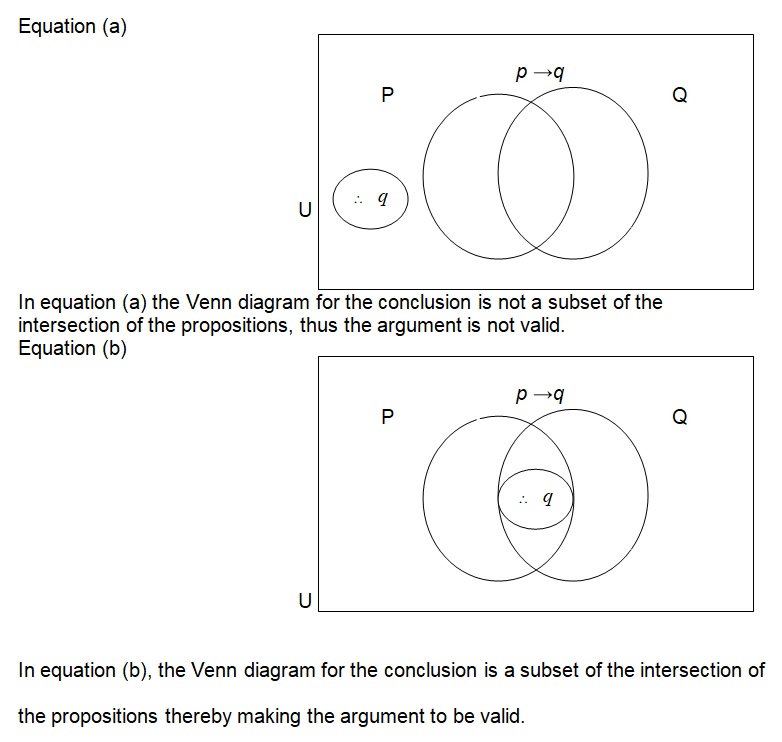
Conclusion
In circumstances that have (p →q), and P has a Truth value (T) while Q has a False value (F), then the (p →q) value will be F (False Value). Also, it is not the worry of logic as to whether the premises are true or false, but with the validity that can be deduced from them. Finally, if the Venn diagram (that is, for the Conclusions) is a subset of the intersection of the propositions, the argument is regarded as being valid.
References
Bluman, A. G. (2005). Mathematics In Our World. College of Allegheny: McGraw-Hill Publishers.
Royden, H.L. (2001). Real Analysis. Web.