“A set is a collection of well defined and well-distinguished objects of our perception or thought.” (Mohindru & Grover, 2003, p.1). Set is usually represented by capital letters and some of the standard sets that are available are
- N [represents set of all-natural numbers]
- W [represents set of all whole numbers]
- C [set of all complex numbers] and so on.
From the book, Naive set Theory in the undergraduate text in mathematics by Paul R. Halmos we can understand that “mathematics is full of examples of sets of sets.” (Halmos, 1974, p.1). A line is a set of points and a set of lines make up a plane and so on. Thus the hold of sets in the field of mathematics is immense. (Halmos, 1974, p.1).
The objects which constitute the set are called the elements of the set. Various operations could be performed on a set such as a union, intersection, compliment of a set, etc. For a better understanding of these concepts let us take an example of two sets, say set A and set B. When we say union of set A and set B we imply a set that has all the elements of set A and set B. The term intersection in this context would give a set of values that belong to both sets. Now suppose U is a universal set and set A is a subset of U then the complement of set A would imply all the values of the universal set U which are not there in set B.
Let us consider a set A that will contain five elements that are essential and let us consider a set B that will have elements that we would like to buy.
Let the elements of set A be {monitor, mouse, joystick, processor, keyboard} and let set B have elements {antivirus, firewall, table, joystick, mouse}. This forms the set of essential items and the items that we would like to buy.
Thus the list of items formed by the union of both sets would be {monitor, mouse, joystick, processor, keyboard, antivirus, firewall, table}. The list of items formed by the intersection of the two sets would be {joystick, mouse}.
Assuming there is only one of each item and the cost of each item to be as follows:
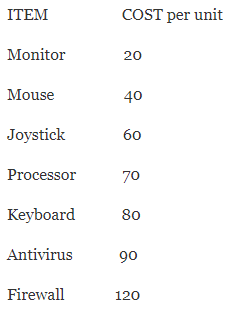
Looking at the table the total cost of set A would be 20 + 40 + 60 + 70 + 80 = 270.
The total cost of the items formed by the intersection of the union of the two sets would be = 20+ 40+ 60+ 70+ 80+ 90+ 120+ 30 = 510.
The total cost of the items formed by the union of the two sets would be 40 + 60 = 100.
Now suppose there are two sets of A and three sets of B.
Then set A can be written as {monitor (2), mouse (2), joystick (2), processor (2), keyboard (2)}.
And set B can be written as {antivirus (3), firewall (3), table (3), joystick (3), mouse (3)}.
Items formed by the union of the two sets would be {monitor (2), mouse (3), joystick (3), processor (2), keyboard (2), antivirus (3), firewall (3), table (3)}.
Thus the cost of the items formed by their union would be = 2*20+ 3*40+ 3*60+ 2*70+ 2*80+ 3*90+ 3*120+ 3*30 = 1360.
Items formed by the intersection of the two of set A and three of set B would be {joystick (3), mouse (3)}.
Thus the total cost of the above-mentioned set would be = 3*40+ 3*60 = 300.
Reference List
Halmos, P R. (1974). Naive set theory: The axiom of extension. Springer.
Mohindru, J P., & Grover, K. (2003). Modern’s ABC of CBSE: Mathematics part-A-core: Sets and elements. Jalandhar: Modern Publishers.