The Neville Theta C function is named after Eric Harold Neville and is mathematically defined as:
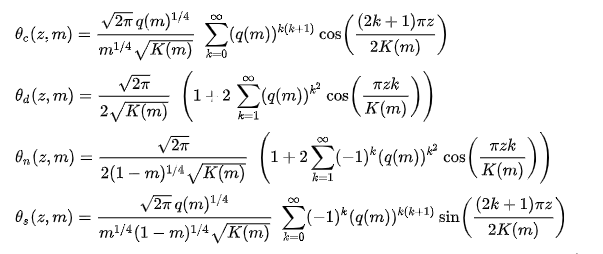
From the formula, K(m) is the complete elliptic integration of the first kind
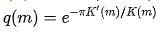is the elliptical nome (Lide 135).It should be noted that the function θp (z, m) can at times be defined in terms of nome q(m) and then written as θp (z, q).
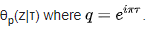
The Neville Theta C function is related to other functions in many ways. For instance, the Neville theta function can be expressed in terms of Jacobi theta functions as shown below:
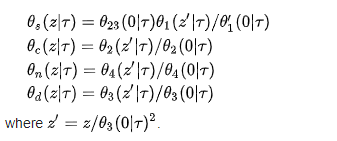
Besides, the Neville theta function can be related to the Jacobi elliptic functions if pp. (u, m) is a Jacobi elliptic function (p and q are one of the s, c, n, d), then
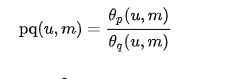
The Neville Theta C function provides a suitable function for both numerical and symbolic manipulation.
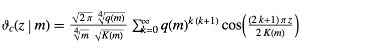
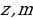}is a meromorphic function of z with a complicated branch cut structure in the 
The symmetry of Neville Theta C function involves a variety of function which individually examines different values. The functions are as follows:
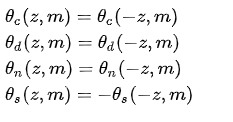
The four elliptic functions are used when developing the symmetry of Neville Theta c function.
Moreover, the Neville Theta c function can be used in making complex 3D plots. When such complex plots are developed, they appear as shown below:
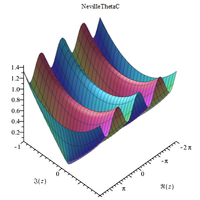
This an excellent example of a Neville Theta C function that has been developed on multiple planes allowing for the exchange of the planar views.
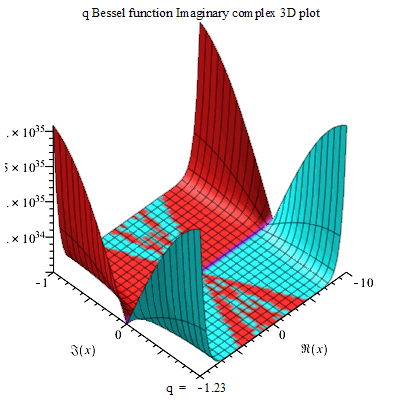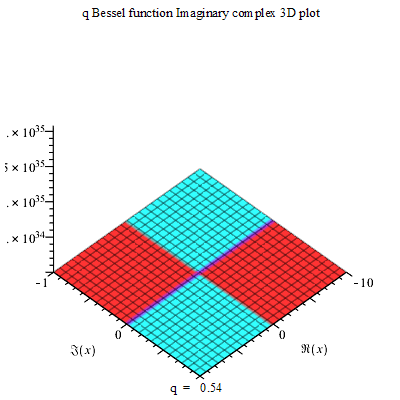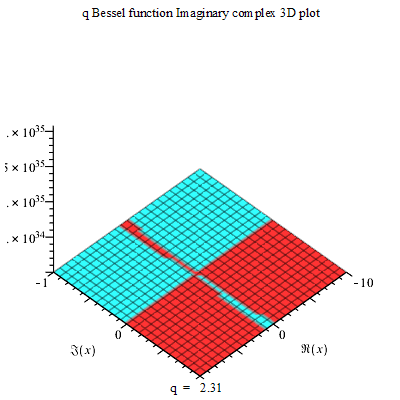
The Neville Theta C function can allow for the formation of a QBessel function abs of a 3D complex structure on a maple plot. Such 3D structure can change its planes on the vertical and axis indicating how progressive plotting can be done (Copson 810).
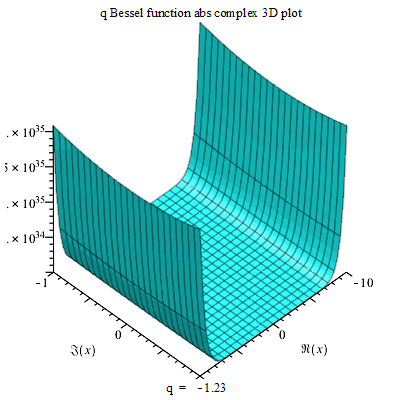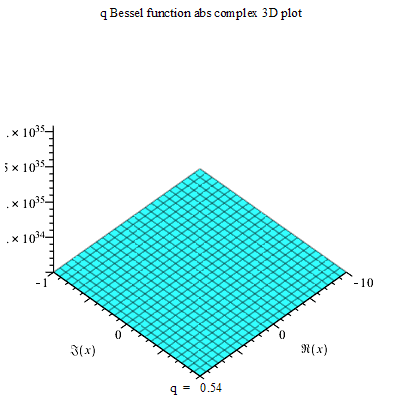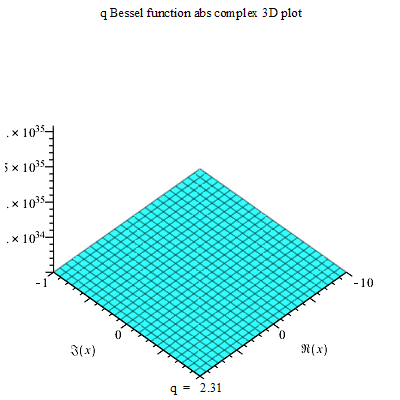
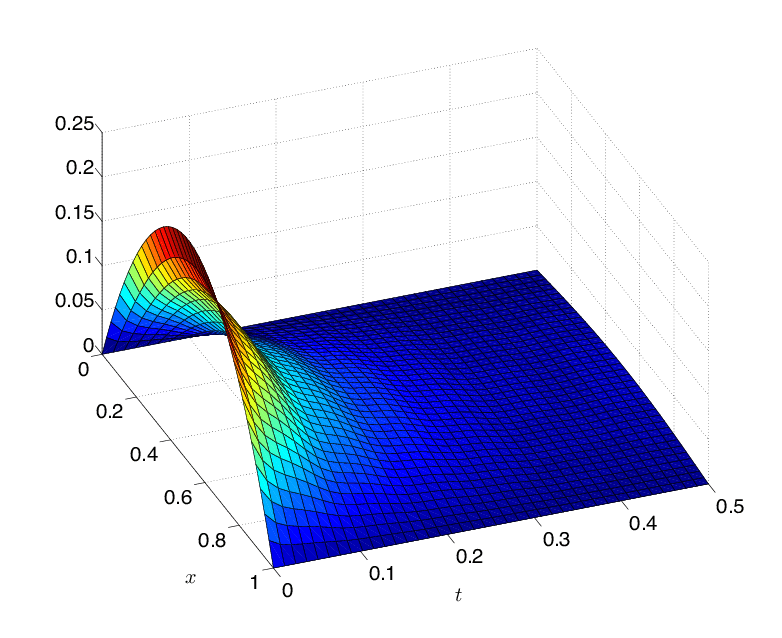
On the other hand, Neville Theta C function allows for the development of an Inviscid Burgers Equation, but this is only possible in a 2D dimension. Besides, related to the Inviscid Burgers Equation is the simulation results for a controlled heat equation. The Simulation result equation can be used in developing a 3D simulation object that rises from both axes on one end but only stationary at another end.
The Neville Theta C function also involves differential equations which are used in solving complex functionalities in math.
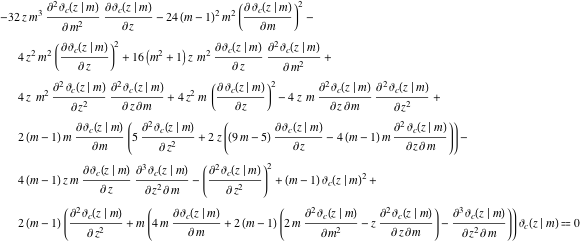
However, despite that the Neville Theta C function involves more of differential equations, it also integrates equations, which can be related to differential equations. In this case, they are providing simulation among functions of integration and differentiation enabling to form the baseline for the two.
Neville Theta C functions are interesting in such a way that, despite the common mathematical functions, they go overboard and are applied in several other disciplines other than mathematics. For instance, as indicated, the functions can be used in making 3D simulation objects which are beyond the comprehension of Math but have greater application like in technology and engineering. The Neville Theta C function grows with complexity as the subjects interchange one another (Copson 817). That is to say, the functions that are used in math are not as complicated as those used in engineering and technology fields as indicated by the figures above. Therefore, this is one of the places where the functions become interesting as it revolves around building of complex structures with significant application.
Moreover, Neville Theta C functions have attained real world application, and, unlike the Jacobian functions, they are greatly used severally in different sectors. For example, in engineering and construction, the functions are greatly used to determine the rising gradients of structures including houses, and other structures like roads, bridges and many more (Abramowitz and Stegun 189). The applications of Neville Theta C enable the developers, first, to determine how the setting should be done if the place is suitable and can carry the whole project, and help to avoid any future perils. Building of ships and other large vessels is also dependent on the application of Neville Theta C functions. Water vessels are among the sensitive structures that require precision. Therefore, with the use of the complex functions of Neville Theta C, it is possible to determine the step by step development of the vessels without any problem of one side being bigger or smaller than the other, and bringing balance (Abramowitz and Stegun 347). Therefore, primarily, these functions are greatly used in building construction and design as one of the real-world applications.
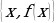
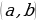
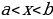
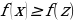
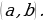
Graphs quite distinctively offer the local minimum and maximum points from their functions (Lozier 107). They are useful in understanding the shape of the graph. When Neville Theta C functions are applied in problems, one may need to determine the smallest and the largest value that the function can achieve (Wolfram Research, 1). The graphs below can help in elaborating the maximum and minimum points.
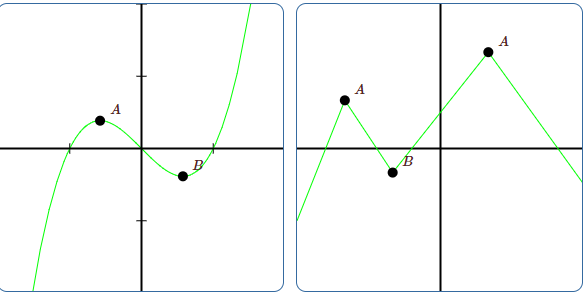
The graphs contain A’s as their maximum points and B’s as their minimum points. However, on the complex application of Neville Theta C functions, it is not easy to determine the maximum and minimum points from graphs or structures that have been developed, especially the motion structures (Wolfram Research, 1). Therefore, in this case, the equations alone are used to determine the maximum and minimum points as these continuously interchange within the motion graph.
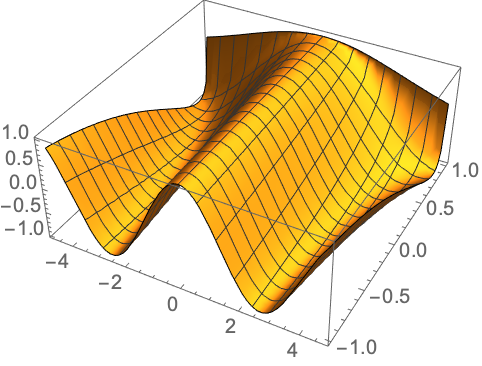
The functions can also be used in plotting over the z-m planes. The equation used in this function is
From this equation, a structure like the following can be obtained.
Besides, it can be applied in rectangular conducting sheets to determine current flow when voltage is applied at a pair of opposite corners (Neville 195). The equation that is used in this case is as follows.
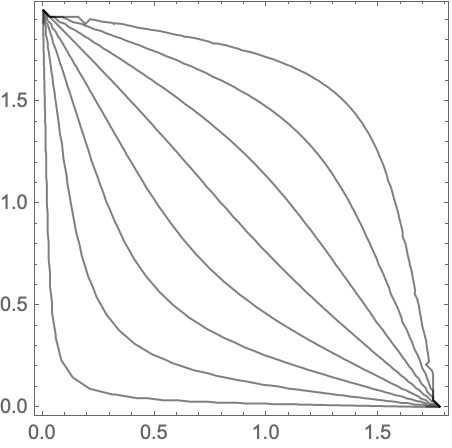
On the other hand, the plotting of the flow lines uses the following equation:
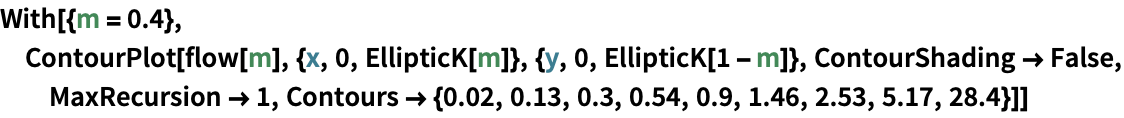
Therefore, the final current flow will be shown as:
In parametrizing a lemniscate by arc length, the function’s equation that is used is:
Thus, this can show the parametrization’s classical and arch length using the equation:
The output will finally be as shown below:
Works Cited
Abramowitz, Milton, and Irene A. Stegun. “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.” US Government Printing Office, 1970.
Copson, E. T. “Jacobian Elliptic Functions.” Journal of Nature Research, vol. 2, no. 8, 1994, pp. 810-810.
Lide, David R. “Handbook of Mathematical Functions.” A Century of Excellence in Measurements, Standards, and Technology. CRC Press, 2018, pp. 135-139.
Lozier, Daniel W. “NIST Digital Library of Mathematical Functions.” Annals of Mathematics and Artificial Intelligence, vol. 3, no.11, 2003, pp. 105-119.
Neville, Eric Harold. “Jacobian Elliptic Functions.” Clarendon Press, 1951.
Wolfram Research. “Neville Theta C; functions.wolfram.com”. 2020. Web.