Financial researchers are focusing on deriving a model that calculates a Q-measure and P-measure distributions. Q-measure focuses on risk-neutral that has a role in pricing. P-measure focuses on real-world that receives more attention than Q-measure. Real-world measures depend on pricing and risks. The modelling process involves the use of potential future exposure measures that uses the same calculations as credit value adjustment. Potential future exposures and other variables, such as equity prices, determine the risk management purpose. The joint measure model ought to determine pricing and quantile measures (Hull, Alexander and Alan 2). Previous researchers concentrated on risk-neutral measure due to its role in pricing. The emergence of credit facilities, pension, and insurance claims shifts research to real-world measures. The joint model aims to use market prices and investor risk preferences as the parameters for input calibration.
The joint model uses the general formula, dr = µ(t,r)dt + δ(t,r)dz, in order to determine the structural movement of pricing and quantile measures (Hull, Alexander and Alan 3). The formula is a derivation from the Girsavno’s theorem and Wiener process. Volatility term δ(t,r) reflects forward-looking of estimates in the real-world process. Therefore, δ(t,r) is an estimate of market implied in computing real-world quantities. In order to obtain the risk-neutral and real-world rates, the model requires continuous measurement of divergence probability data for over the horizon of 30 years. The divergence magnitude depends on µ(t,r). In some situations, δ is a constant in the equation, hence making µ an independent variable. Figures 4 and 5 are graphical examples of the joint model formula that estimates the historical market price of the United States interest rates for the past 5 and 30 years. The results of the joint measure model will get analyzed on the basis of Hull and White model.
Volatility rates of the joint measure model differ greatly according to calculations from January 1982 to January 2014 (Hull, Alexander and Alan 6). The changes in volatility rates affect the market prices due to changes in the risk estimates and interest rates. The construction process of the joint measure model requires high subjective assumptions so that λ may measure estimates over long time periods. The λ assists in adjusting risk-neutral and real-world rates in all market conditions. The approach of using λ requires use of additional estimate for future expected short rates. The final formula for constructing the joint measure model is as follows:
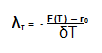
λT represent the market price of interest rate risk in a given time (T), T represents time, r0 represents long-run average short-term interest rate, F(T) represents long-run average instantaneous future rate, and δ is a constant.
Figure 4 and 5 are graphical representations of the probability distribution (y-axis) versus interest rates (x-axis). The graphical representation in figure 4 shows the probability distribution within the range of 5 years versus short-term interest rates (Hull, Alexander and Alan 15). The graph in figure 5 shows the probability distribution within the range of 30 years versus short-term interest rates (Hull, Alexander and Alan 16). The two graphs show consistency of the means of the short rate estimates in the real-world process. The bar graphs show good relations between historical data (real-world) and market prices (risk-neutral). The results of the graphical models are similar in graphs 4 and 5 because of the consideration of one-factor that provides risk-neutral process, calibrated same as structured data. The average long-run interest rate on the two graphs is 4.30% that corresponds to the probability value of 5%. This means the probability distributions of 5 and 30 years are similar. The extreme rates of the graphical representations of the graphs 4 and 5 are very high and very low due to the passage of time (Hull, Alexander and Alan 8).
Work Cited
Hull, John, Alexander Sokol, and Alan White 2014, “Modeling the Short Rate: The Real and Risk-Neutral Worlds,” Web.