Introduction
One of the most sensitive areas of research is statistical analysis because the output interpretation of the results depends on their reliability and validity. Many academic studies aim to use quantitative methods of measurement to gather initial results and, from them, draw conclusions about the nature of the phenomena being determined and the correlations between the variables. In this context, it is evident that it is the task of any researcher to achieve standards in which the results obtained to meet the criteria of high reliability, reproducibility, and validity. To do this, authors must be familiar with common statistical errors and unique concepts, among which Simpson’s Paradox deserves special attention. In brief, such a counterintuitive phenomenon defines a scenario in which combining samples leads to the formation of an altered or opposite pattern that is true for each of the samples individually (Grigg, 2018). This essay aims to discuss the Simpson Paradox effect in detail, as well as define the idea and practical implementation of the latent variable. The paper is an up-to-date summary of the available scholarship and is, therefore, a valuable read for students in the course as well as anyone interested in the concepts of statistical analysis.
Main body
Often the adverse effects of Simpson’s paradox are encountered by authors when conducting research on sociological measurement. As it is known, one of the most effective and visually accessible methods of demonstrating results is the correlation model, which uses linear regression tools to draw conclusions about the nature of the relationship between two variables. If, as such a result, the authors get a seemingly clear picture of a strong positive relationship in which an increase in one variable leads to an increase in the other as well, this does not mean that objective reality is reflected correctly. Indeed, it sometimes happens that the categorization of generalized data into separate groups shows the exact opposite picture: a strong positive regression is replaced by a negative one (Obrazcova, 2020). As a result, conclusions based on generalized data are entirely inconsistent with high research standards and lead to incorrect conclusions. This discrepancy, or inconsistency, forms the basis of the idea of Simpson’s Paradox.
The significance of this effect is hard to deny, especially in those studies that examine fundamental problems or issues related to national, food, and health security. Such a breach of logic, not noticed by analysts when interpreting it, can have very serious negative consequences for the community as a whole, not just for the reputation of the individual researcher. In fact, Simpson’s Paradox serves as a reminder that any causal relationships that are initially discovered in an experiment must be subjected to critical evaluation. Failure to do so raises the possibility of false or inaccurate conclusions, which cannot have any positive effects. Another illustration of the high importance of the Simpson Paradox to the academic community is the tacit recognition that statistics rarely remain unchanged and conservative. On the contrary, if one examines them from a different angle or modifies the set of controlled variables, the patterns and generalizations previously found may no longer be relevant. As a result, Simpson’s Paradox is a critical idea of exact statistics, reflecting the unacceptability of superficial interpretations for any serious study.
It should be emphasized that several mathematical operations can inadvertently lead to the manifestation of Simpson’s Paradox at once. In the first place, as was shown above: when data differentiated by categories have their own dependencies, and when generalized, lead to a new result. Thus, the operation of summarizing individual cohorts must be performed with great care. On the other hand, the result need not necessarily be reversed. Sometimes it happens that when the disjointed data are combined, the final correlation decreases or increases, but the overall direction remains the same as it was for the individual data. Although at first glance it may seem that such manifestations of the Simpson Paradox are not critical, in the most sensitive branches of knowledge, whether in clinical dosage studies or engineering calculations of missile direction, such errors can be decisive.
To fully understand the principles of inconsistency in combining data, emphasis should be placed on the idea of latent variables. Students generally know from statistical theory that there are independent, dependent, and even control variables: all of which are used in making measurements of any patterns. Moreover, both control and independent variables lend themselves to manipulation by the authors in order to more extensively explore the nature of the relationship between quantities. Although each of the three types of variables mentioned is available for observation or counting, latent variables reflect the opposite concept. In more detail, latent variables are commonly referred to as those quantities whose state cannot be estimated from directly observable signs. For this reason, to determine latent variables, it is common to use external data that have a semantic relationship with the latent variable and indirectly allow to estimate it. However, to achieve improved accuracy of the results, it is recommended to use a set of several alternative attributes that help to judge the nature of the latent variable.
By the present moment, when the central core of Simpson’s Paradox and the idea of the latent variable have become explored, an illustrative example of their applicability in a business practice should be considered. For this purpose, it is acceptable to use the example of website conversion. First of all, it should be noted that conversion is understood as a ratio that reflects the proportion of site visitors who performed a targeted action to the total number of all guests (Smith, 2021). In the context of the business scenario under discussion, the targeted action consists of making a purchase on the e-store website. This evaluates the relationship between the purchase of a product and a visit to the product description page. It is expected that studying the description prevents the purchase of the product. More specifically, the following picture may emerge in front of platform analysts during the measurement time:
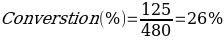
These data clearly reflect several facts. First of all, the mobile version is a more popular platform for visiting an e-store than the desktop. However, more intriguing is the data which shows that visiting the product description page in both cases led to an increase in the conversion rate. Consequently, it is possible to conclude that this section of the online store web page is helpful and requires the attention of marketers. However, when trying to combine the data when differentiation by the platform is not of interest, a generalized table is obtained:
Therefore, from the summary table, it is not possible now to conclude longer which shopping platform is more relevant for users. More remarkably, numerical aggregation of the data led to the opposite conclusion: conversion is higher for those users who did not visit the web section. This is an example of Simpson’s Paradox because, in this case, the measurement aggregation procedure led to an erroneous judgment, which means the marketing strategy would have been built incorrectly. For example, the store management department might have stopped funding the product description sections because it would have felt that it had a detrimental effect on product purchase. In reality, the effect is the opposite, and the division of products into groups clearly reflected this trend. It is also easy to see that the hidden variable in this example is the platform through which the purchase is made. Without categorization, it would have been impossible to arrive at the correct results, but using differentiation based on the latent variable allowed for doing so.
Conclusion
To conclude, statistical analysis requires much effort from authors because it must meet criteria of high reliability, quality, and validity. Simpson’s paradox is a concept that is reflected in practical statistics: researchers can arrive at false results when combining data. In doing so, the final interpretation can either be altered or the exact opposite. In any of these cases, the negative effect of such distortion is noticeable, primarily if the research is conducted in sensitive areas of knowledge. To prevent such scenarios, it is necessary to critically evaluate the causal relationships found and look for hidden variables that can change the interpretation qualitatively.
References
Grigg, T. (2018). Simpson’s paradox and interpreting data. TDS. Web.
Obrazcova, I. (2020). Simpson’s Paradox and segmentation: Why analysis is crucial. WA. Web.
Smith, L. (2021). What is conversion: definition, formulas, and examples. Snov. Web.