Introduction
Coming to the centre stage of self-propelled motion, the innovation of scooters has revolutionized self-drive transport a big deal. Scooters come in various designs suited for different functions. The different designs are geared towards enhancing speed, flexibility, stability as well as manoeuvrability among other adaptations. It is under this context that scooters are classified as folding scooter, executive scooter, freestyle scooter, skateboard scooter as well as based on the number of wheels (Murphy and Corbett, 2005). Cutting across these designs, scooters can either be human-powered (kick scooters) or motor-powered (power-operated scooters). Even with the diversities in designs, knowledge in understanding the basic principles of the designs is what matters. The different designs integrate different physics principles to enhance their adaptability for diverse riding skills. Of our particular interest is a flat four-wheeled scooter board which has a unique design meant for trick riding (Martin, 2002). A flat four-wheeled scooter board merges different physics concepts to suit its applications under motion or when stationary. Our quest in understanding how these concepts are integrated into the design leads us back to appreciating the different physics laws as applied in a flat four-wheeled scooter board. The laws and forces that play a big deal include Newton’s laws of motion, gravitational forces, and centripetal forces among others.
The general features of a scooter are a handlebar, the deck, and the wheels. The wheels are always small in size and are primarily made up of aluminium material. The deck is normally designed to enhance the steering of the board. On considering the functionality of the deck as a steering mechanism, we encounter two designs of the deck that enhance this application. We have a ‘deck-tilt-controlled steering’ and a ‘lateral-force-controlled steering’ (Murphy and Corbett, 2005). These have their own merits and demerits as regards stability, flexibility, turning radius, and speed notwithstanding. For instance, while the former design is unstable and uncomfortable at high speed, the latter is the direct opposite. It is stable under motion and unstable when stationary (Edwards, 1998). A flat four-wheeled scooter board utilizes a ‘deck-tilt-controlled steering’ design while ‘lateral-force-controlled steering’ is reserved for scooter boards that have wheels mounted along a single line. The designs of these scooter boards give a rider a host of preferences as per the rider’s expectations. A good board on the market will always achieve its properties only after utilizing the basic theories which have a bearing on the underlying physics principles. A focus on a scooter at rest, under motion on a horizontal plane, under motion along an inclined plane and, the deck-tilt controlled steering forms the basis for discussion for this paper. This will give us an insight into understanding the physics principles behind a four-wheeled scooter.
A four-wheeled scooter board at rest supporting a rider
A scooter at rest supporting a rider exhibits Newton’s third law of motion which states that “for every action, there is an equal and opposite reaction force” (Edwards, 1998). Considering figure 1 below, the forces acting on the scooter along the vertical axis are gravitational force (Mg) which is directed towards the centre of the earth and the reaction force acting perpendicularly upwards on the tyres. Since the body is at rest, the resultant horizontal force is null since the static frictional force between the tyres and the ground is commensurate to an opposite force due to an external influence. Furthermore, at rest, the momentum of the scooter board is zero since the velocity is zero. It is therefore obvious that the impulse is also zero as there is no change in momentum.
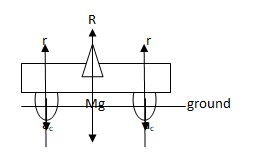
Action force = total mass (M) of the rider (m1) and the weight of the scooter (m2) x gravitational acceleration (g). The total reaction force, R, is the total sum of all the reaction forces, r, as applied by the tyres.
A flat four-wheeled scooter board at rest without a rider
Considering the scooter board above without a rider, the magnitude of forces along the horizontal axis will be constant i.e. they are opposite and equal and thus, they cancel out maintaining it at rest. On the contrary, the magnitude of forces plying along the vertical axis will change though maintaining Newton’s third law of motion. This is to say that the action and reaction forces will change to m2g. The momentum and impulse will be intact (Crowell, 2010).
A scooter in motion on a flat horizontal plane supporting a rider
A four-wheeled scooter board under motion experiences several forces that ply along two axes i.e., the horizontal and the vertical axes exhibiting Newton’s laws of motion. Of the important law familiar with bodies under motion is Newton’s second law of motion. This law states that “the acceleration of a body resulting from an applied force is proportional to that force and inversely proportional to the mass of the body” (Murphy and Corbett, 2005). That is to say that the force (F) is equal to the product of total mass (M) and acceleration (a) i.e. F=Ma. A scooter in motion moves forward due to resultant forward force (FR). The external force (F) is greater than the friction force (Fr) acting on the tyres and thus the scooter moves forth due to the resultant force. The friction between the tyres and the ground aids in the forward motion as fulfilled by Newton’s second law of motion as shown in figure 2 below. Mentioning this law gives us a reflection of Newton’s scooter. The scooter is propelled forward thanks to a balloon fitted at the back expelling the air backwards (action) and hence, a forward motion results due to the reaction force on the balloon (Hewitt, 2000).
The scooter starts from rest with an initial velocity (u) and then moves at a final velocity (v) after the time (t). The body experiences an impulse due to change in momentum (Δp):
From the first equation of linear motion, a= (v-u)/t
And, F=Ma, therefore,
Impulse=Ft =Mv-Mu
From rest, the rider will surge backwards due to inertia as a result of the tendency of the body to resist change. The opposite will happen when the scooter comes to rest when the rider surges forth.
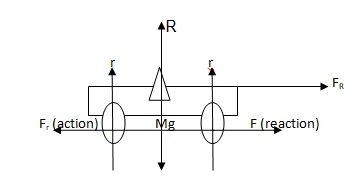
A scooter in motion on a flat horizontal plane without a rider
Consider Fig 2 above without a rider. The change in overall mass from M to m2 means that several components of the forces have to change. R changes to m2g and FR changes to m2a meaning that a small force will be required to give the same acceleration. Furthermore, the momentum changes to m2v revealing a decrease in impulse considering the body starting from rest.
A four-wheeled scooter on an inclined plane
A scooter in an inclined plane has several components of forces along the axes resolved. The resultant components of the forces are responsible for the stability of the rider. This is where the functionality of the tilt deck comes in handy. The rider strives at making the deck parallel to the plane to prevent slipping off. Consequently, the resultant normal reaction force due to the tyres changes to Mg Cos α while the lateral frictional force changes to Mg Sin α. This portrays that on an inclined plane the lateral frictional force between the tyre and the ground increases with the gradient as the normal reaction decreases (Hewitt, 2006). It is, therefore, significant to ride on a scooter having tyres that have well-defined threading patterns to avert accidents due to skidding. Figure 3 below shows how the forces are resolved along an inclined plane.
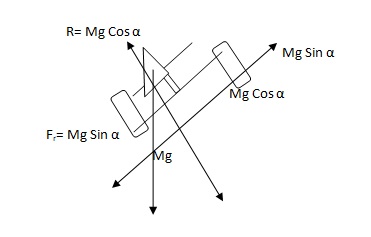
The equal and opposite lateral frictional forces on the tyres keep the scooter intact on the ground preventing slip-offs.
Another area where the deck comes in handy is during steering. The turning radius of a scooter is dependent on the velocity (v) of the scooter and the angle of tilt (α) of the deck relative to the horizontal plane. An optimal turn can be achieved at a specific designated optimal speed. It is however apparent that the centrifugal acceleration is heavily dependent on the velocity of the scooter. It, therefore, follows that a scooter board with four wheels at high speed will often overwhelm the rider in terms of control (Agatha, 2000). They are bidirectional and unstable at high speed.
Conclusion
Essentially, the general design of a four wheeled scooter board utilizes the fundamental principles and laws of physics. To achieve optimal functionality as regards scooter boards, a manufacturer should be able to integrate the different principles under a given design of the board. Understanding how these forces ply along different axes over diverse slopes when at rest or under motion have a bearing on the optimal adaptability of a scooter board for a given functionality. However, these principles are not only a reserve for manufacturers, but they are also vital for a rider especially when it comes to steering and negotiating sharp bends.
References
Agatha, C. H. (2000). Systems, Experts, and Computers: The Systems Approach in Management and Engineering, World War II and After. Sydney. Dibner Institute press.
Crowell, B. (2010). Conceptual physics: Conservation laws. Chicago, IL: University of Chicago Press.
Edwards, Q.S. (1998), Systems Analysis and Policy Planning: Applications in Defense: New York, NY: New York University Press.
Hewitt, P.G. (2006).”Conceptual Physics: Practicing Physics”. London: Oxford University Press.
Martin, J. (2002). Cold War Laboratory: RAND, the Air Force, and the American State. London: Oxford University Press.
Murphy, T. & Corbett, B. (2005). “Quadrasteer Off Course: Wards Auto World”. Web.