Abstract
In this work, an experiment was conducted to establish the relationship between the range and time of flight of a cannonball as a function of its initial velocity of departure from the cannon. It was determined that the cannonball would fly farther and longer if the initial velocity was higher at a fixed angle of inclination. The virtual simulation data was recorded and analyzed using MS Excel.
Introduction
Background: The trajectory of the cannonballs is not linear but instead a parabolic shape. It is clear that the range and altitude of cannonballs, as well as the time in flight, are functions of initial characteristics, so we cannot expect cannonballs with different initial velocities for a given angle cannon inclination will end up at the same point.
Purpose: The purpose of this laboratory work was to test the relationship between the initial launch velocity of a cannonball and dependent factors, including range and flight time.
Hypothesis: The greater the initial velocity was given, the farther the cannonball could fly and, as a consequence, the more time in flight was required.
Materials and Methods
Online Simulator PhET: Projectile Motion
The laboratory experiment was performed virtually using the Phet online simulator, in which the user had the ability to adjust and fix the variables of the experiment manually. Expressly, in the Lab section, the angle of flight of the cannonball was set to 60°, and a cannonball with a constant mass of 17.6 kg and a diameter of 0.18 m (PhET, n.d.) was used as the object. Air resistance was not considered in the present experiment, and the acceleration of free fall was a constant value. The variable factor was the initial launch velocity of the cannonball: this ranged from 10 to 30 m/s in 2 m/s increments. The launch button activated the cannonball flight, and the range of its fall was measured with a built-in ruler. Time measurement was also realized using the built-in ruler function.
Results
Table 1. Summary data on range and flight time as functions of initial velocity
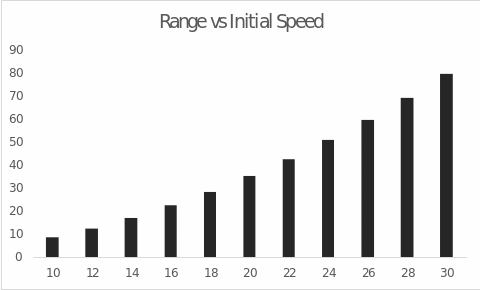
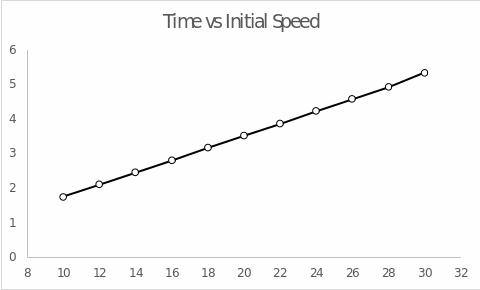
Discussion
The purpose of the present experiment was to determine the relationship between the range and flight time of cannonballs as functions of their initial launch velocity from the device. The initial hypothesis was that the greater the initial velocity, the farther the cannonball would arrive and the longer it would take to fly. Referring to the obtained data, reflected visually in Fig. 1 and Fig. 2 perfectly demonstrates these patterns. An increase in the initial velocity naturally increased both the flight range and the time required for landing. This fully confirms the hypothesis and postulates a linear relationship between the variables. Based on these data, we can assume that continuing to increase the initial velocity at a fixed angle of inclination will maintain a linear trend, and even increasing this velocity to a maximum value will not affect the change in trajectory or detected patterns (Rajai, 2021). Notably, each flight followed a strictly parabolic trajectory, and the shape of this parabola, including branch width and peak height, again depended on the initial launch velocity.
Conclusion
To summarize, the parabolic flight of the cannonball depends on the initial settings of the cannon. The flight range and the time taken to land depend entirely on the initial velocity of the cannonball at a fixed angle. The higher the velocity of departure, the farther and longer the cannonball flew, and vice versa; the parabolic shape of the trajectory was maintained for all cases. The current experiment can be extended by changing the angle of the cannon and assessing how much of an effect this has on the range.
References
PhET. (n.d.). Projectile Motion. Web.
Rajai, A. P. (2021). How to calculate projectile motion. Lambda Geeks. Web.