Friday the 13th Superstition and Consumer Behavior

How do superstitions regarding Friday the 13th affect human behavior?

Data are given

The number of shoppers in nine different super markets in southeast England is recorded on Friday the 13^th and Friday the 6^th between July 1990 and November 1992. The British department of transport is the source of the data.

Aim

To test that there is any difference in the shopping pattern of the people on Friday the 13^th and Friday the 6^th.

Variables

The variables involved in this test are shopping data set, Date, and location. The variables of date, location are independent and the shopping data set is dependent. The test is to analyze that there exists any dependency between the shopping data set a variable and the variable of dates.

Statistical test

The most appropriate statistical technique to test the hypothesis for this situation is the paired t-test. The samples are random but dependent on each other. The shopping data set was recorded for the same location for two various dates. Hence the samples are dependent. So we have to use the paired t-test.

Hypothesis Testing

Null hypothesis: There is no difference between the shopping pattern on Friday the 13^th and Friday the 6^th.

Alternate hypothesis: There is a significant difference between the shopping pattern on Friday the 13^th and Friday the 6^th.

H₀: µ₆ = µ₁₃ vs H₁: µ₆ ≠ µ₁₃ where µ denotes the population means of the number of shoppers and the suffix denotes the dates.

Level of significance: As no level of significance is specified the default value of 5% is considered.

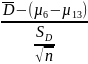Test Statistic: Under H₀,  ~ t_{n – 1} where D denotes the differences S_D denotes the sample standard deviation and n denotes the sample size.

From the data set given, the mean number of peoples on Friday the 6^th is 4970.51, the mean number of peoples on Friday the 13^th is 5017 and the number of samples is 45.

Hence D = Difference between the sample means = 5017 – 4970.51 = 46.49.

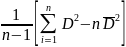S_D² =  = (1444470 – (45 × 46.49² )) / 44 = 30618.422

S_D = 174.98

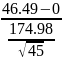Substituting the values in the test statistic,  = 1.782

Degrees of Freedom: The degree of freedom is n – 1 = 45 -1 = 44.

Result: The critical values for the test are +2.32 and -2.32 as the test is two-tailed. Since the obtained value 1.782 lies between the critical values, we have no evidence against the null hypothesis and it is reasonable to conclude that there is no difference between the shopping pattern on Friday the 13^th and Friday the 6^th.