Gottfried Leibniz is one of the greatest polymaths as scholars credit him with several inventions in various fields, including mathematics, psychology, metaphysics, law, physics, and engineering. He was born on July 1, 1646, in Leipzig, Germany. This biography seeks to look at his life story and his multiple discoveries and influences in several fields, even though recognition for most of his work came later in life as they were published in the early twentieth century.
Leibniz’s parents were Friedrich Leibniz, his father, a philosophy scholar and professor at Leipzig, and Catharina Schmuck, his mother. His father Friedrich passed away when Leibniz was six years of age, and his mother brought him up, from whom he learned religious and moral principles from her, which later played a critical life in his philosophy and life (O’Connor and Robertson). He got into Nicolai School in his hometown of Leipzig at the age of seven, where teachers taught him Latin.
At the age of 12, he taught himself Latin that was way ahead of the school’s syllabus (O’Connor and Robertson). His teachers trained him in Aristotle’s Logic and classified knowledge in school, which he was not content with. As a result, he started coming up with ideas on how to improve it (“Gottfried Wilhelm Leibniz”). Leibniz was interested in his father’s writings, although he also read books on metaphysics and theology from Protestant and Catholic books.
In 1661, at the age of 14, he got into the University of Leipzig and studied Mathematics, Philosophy, Greek, Hebrew, and Latin. At the university, he was regarded as a prodigy and outshined his contemporaries (Burton). Two years later, in 1663, he graduated with a Bachelor’s degree after defending his thesis titled De Principio Individui (O’Connor and Robertson). He passed his summertime by attending mathematics classes at the University of Jena but returned to Leibniz to start working on his legal studies.
After Leibniz got awarded his master’s degree in philosophy, his mother passed away. He was offered a teaching position at the Faculty of Philosophy at Leipzig after qualifying by writing Disputatio Arithmetica de Complexionibus, which he later expanded in 1666 to Ars Combinatoria (“Gottfried Leibniz”). In this work, Leibniz discussed the invention of new mathematics, like a language of reasoning, referred to as Characteristica Universalis, from which scientific concepts could be formed (Burton). In 1666, he applied for a law degree doctorate, but the Leipzig faculty rejected his application because he was too young, though some say it was out of jealousy (Burton). Following the rejection, Leibniz applied to the University of Altdorf and, the following year, received his doctorate from the university for his dissertation titled De Casibus Perplexis.
Leibniz refused to work at Altdorf; instead, he worked at the Nuremberg alchemical society as its secretary before meeting Baron Boineburg, who offered him a job in Frankfurt in November 1667. Over the next couple of years, Leibniz worked on some projects, including political, scientific, and literal (O’Connor and Robertson). He relocated to Mainz, where he continued with his law career, with one of his responsibilities to advance the Roman civil code for Mainz (“Gottfried Wilhelm Leibniz”). Leibniz started studying motion, although he wanted to explain the results of elastic collisions.
In 1671, he published Hypothesis Physica Nova, where he asserted motion depended on the spirit’s actions. Leibniz wished to go to Paris to get the opportunity to meet more scientists(O’Connor and Robertson). To get to Paris, he started working on making a machine that could calculate (Schwartz). At the time, the French were planning to attack German areas and plan to convince the French to attack Egypt (Francke). Due to this plan, Boineburg allowed him to visit Paris to persuade Louis XIV not to attack German areas. Leibniz was first to make contact with the Government in Paris. Still, while waiting for the chance, he met several philosophers and mathematicians, including Arnauld and Malebranche, and discussed church reunification issues.
In 1672, under Christiaan Huygens, Leibniz studied physics and mathematics and looked at Saint Vincent’s writing on summing series, where he made several discoveries. In 1673, Leibniz visited the Royal Society during a visit to England, where he demonstrated his incomplete calculating machine (Glowienka). During his visit to the Royal Society, he met some scholars, including Robert Hooke, Robert Boyle, and John Pell. During his conversation with John Pell, Pell advised him to look at Gabriel Mouton’s book, which Leibniz did the next day.
While returning to Paris, Leibniz realized that he had little knowledge of mathematics and that he had to double his efforts. During his study under Christian Huygens, Leibniz asserted that he could find the sum of an infinite series provided that the series could converge (Burton). Huygens tested the formula by trying to determine the sum of the reciprocal of the triangular number as in Equation 1 (Burton):
Equation 1
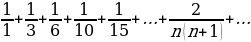
Using the method of expressing each term as the addition of two others as shown in equation 2 (Burton):
Equation 2
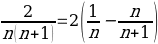
Leibniz goth the sum required by Huygens the equations 3, 4, and 5(Burton) below:
Equation 3
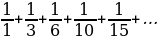
Equation 4
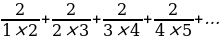
Equation 5
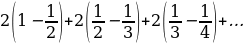
At the same time, Leibniz made a model that was functioning of the calculating machine that improved the device constructed by Pascal (Schwartz). The upgrades included functions such as multiplication and division by repeatedly adding and subtracting (Burton). Leibniz was able to obtain alternating series that he invented, referred to as the Leibniz formula as shown in equation 6 (Burton):
Equation 6
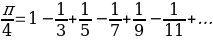
On April 19, 1673, Leibniz got elected to The Royal Society of London as a fellow. He began working on infinitesimal geometry and corresponded to Oldenburg at the Royal Society (Francke). Leibniz got a reply from Oldenburg that Isaac Newton and James Gregory had discovered general methods (O’Connor and Robertson). During this time in Paris, he came up with the basic calculus features he struggled to establish notations. On November 21, 1675, Leibniz wrote a paper for the first time using the symbols
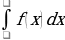
, which also had the product rule for differentiation.
In autumn of 1676, he discovered
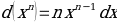
fractional and integral n. Leibniz had a back and forth with Isaac Newton, who believed Leibniz had stolen his calculus methods. His concepts on differential integral never had the idea of limits, with dy/dx thought of as quotient and his integral as a sum. He published his work on calculus simultaneously with Isaac Newton; however, his work was deemed superior to Newton’s.
In 1676, Leibniz left Paris for Hannover after being Librarian and Court Councilor of Hannover, where he spent the rest of his life. The job offered him ample time to work on research more on mathematics. He started working studying and researching geometry, physics, and mathematics (“Gottfried Leibniz”). Scholars note Leibniz as one of the best logicians, with his logic summarized as all ideas get compounded from a small number of simple ideas that form human thought. The second summary is that complex ideas come from simple ideas by asymmetrical combinations analogous to arithmetical multiplication.
One of the most outstanding achievements by Leibniz in Mathematics is the advancing of the binary system, which he improved in 1679. Leibniz did not publish the improvements until 1701 through the writing titled Essay d’une nouvelle science des nombres (O’Connor and Robertson). The binary system he developed is critical as it is the basis of the current digital systems where computers understand and process instructions based on 0’s and 1’s. It is important to note that the binary system’s invention got made in ancient China, and Leibniz only developed it. He developed methods of solving linear equations and other mathematics works that he never published through his work on determinants.
In his paper, Acta Eruditorum, published on October 16, 1684, he expressed a method of finding minima and maxima and drawing tangents for curves. Leibniz also worked to perfect his metaphysical setup when trying to decrease understanding to an algebra of thinking (Ball). He published Meditationes de Cognitione, Veritate et Ideis, whose content was on the knowledge theory, and wrote Discours de métaphysique on metaphysics (O’Connor and Robertson). Scholars also credited Leibniz with the idea that the earth was initially molten.
In Physics, Leibniz came up with a theory of motion and disagreeing with Isaac Newton somehow. Potential energy and kinetic energy were the base of his views, which put forward space as relative, while Isaac Newton put forward that space was absolute. Leibniz argued that space and time are relationist and exist between objects against Isaac Newton’s view that space and time were separate and independent entities. With current knowledge of space and time, Leibniz’s theory on space and time was more favorable than Isaac Newton’s.
The Quantum mechanics principle invoked Leibniz’s indiscernible identity on sufficient reason has recently been used in cosmology. In 1906, Garland published Leibniz’s writing which had many inventions that made him called the father of applied science. Though some of them are not yet translated, his published works included studies on mechanics, forces, and weights that lead to the development of hydraulic systems. Other works include a calculating machine, lamps, clocks, windmills, submarines, and a water pump (“Gottfried Leibniz”). He also proposed desalinating water in the works, removing salt from salty water to make it safe for drinking.
Leibniz was an advocate for forming various scientific societies that followed the format of the French and British Royal Societies. In his correspondences with other scholars, he urged scientific institutions in Vienna, Berlin, Saint Petersburg, and Dresden. However, only one of them came to fruition which was the Berlin Academy of Sciences. Leibniz was considered a polymath due to having a footprint in many fields (Glowienka). From mathematics, law, philosophy, psychology, social sciences, and natural sciences. This work is indeed an incredible feat as he left a mark in every field he decided to research and study.
On November 14, 1716, Leibniz passed away after being sick with arthritis and grout in Hannover. Posthumously one of the questions that have lingered on people’s minds is who between him and Isaac Newton invented calculus, with much of Europe doubting whether Leibniz did it independent of Newton’s work. His work on history, law, and diplomacy has also seen several scholars take a keen interest.
Works Cited
Ball, W. W. Rouse. Short Account of The History Of Mathematics. Dover Publications, 2012.
Burton, David M. The History of Mathematics. 7th ed., Mcgraw-Hill, 2011.
Francke, Christoph Bernhard. “Portrait Of Gottfried Leibniz, By Christoph Bernhard Francke, C. 1700”. The Core Curriculum, 2021, Web.
“Gottfried Leibniz”. Lemelson.Mit.Edu, 2021, Web.
“Gottfried Wilhelm Leibniz”. Plato.Stanford.Edu, 2013, Web.
Glowienka, Edward W. “Gottfried Wilhelm Leibniz (1646-1716)”. Iep.Utm.Edu, 2021, Web.
O’Connor, J. J., and E. F. Robertson. “Gottfried Wilhelm Von Leibniz”. Mactutor, 2021, Web.
Schwartz, Oscar. “In The 17Th Century, Leibniz Dreamed Of A Machine That Could Calculate Ideas”. IEEE Spectrum, 2019, Web.