Probability is the likelihood that an event will occur in the future. The creation of the mathematical theory of probability by Blaise Pascal and Pierre de Fermat was preceded by a gambler’s dispute in 1654 (Franklin, 2015). The point is, a well-known player Antoine Gombaud asked Pascal whether or not to bet money on the occurrence of at least one “double six” during 24 throws of a pair of dice. Though betting on such a combination would be profitable, its probability needed to be calculated. To answer Gombaud’s question, Pascal exchanged letters with Fermat to develop fundamental principles of probability theory. During the 17th century, major contributions to this theory were made by Jacob Bernoulli and Abraham de Moivre (Franklin, 2015). Pierre de Laplace was the first to apply the theory of probability to scientific and practical problems. Since then, the concept of probability became intensively utilized in various fields of knowledge.
The theory of probability is a statistical method that is used to measure the likelihood of occurrence of a future event or outcome. Probability can be calculated by dividing the number of favorable outcomes by the total number of possible outcomes. If P(A) is greater than P(B), this means that event A is more likely to occur than event B. Advantages of this technique include its simplicity, unbiased estimates, and the possibility to compare probabilities. However, disadvantages also exist since it is assumed that each event has an equal chance of occurring and no additional knowledge is taken into account.
Two major categories of probability interpretations whose adherents possess conflicting views about the fundamental nature of probability are physical (objective) and evidential (subjective) probabilities. Objective probability refers to the probability that something will occur based on a recorded observation (Gan, Ma, & Xie, 2014). An example of objective probability is the probability of a coin landing heads up if one flips it 100 times and records each observation. Subjective probability is the probability based on a person’s estimate of an event and its likely outcome. An example of subjective probability is asking football fans about the chances of their favorite team winning the Champions League.
Based on the survey, the probability that a randomly selected American has never been tested can be calculated by dividing the number of Americans who have never been tested by the total number of Americans. The formula for calculation and the result of the calculation will be as follows:
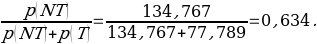
The probability of 0,634 means that out of 1000 American adults, 634 have never been tested for HIV.
To calculate the proportion of 18- to 44-year-old Americans who have never been tested for HIV, one should know two values. The first one is the number of Americans in this age group who have never been tested for HIV, and the second one is the total number of people aged from 18 to 44. The formula for calculation and the result of the calculation will be as follows:
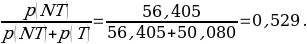
The probability of 0,529 means that out of 1000 American adults aged from 18 to 44, 529 have never been tested for HIV.
In summary, probability is the measure of the likelihood that an event will happen. During the history of theory development, the application of probability moved from games of chance to scientific problems. Two broad categories of probability interpretations, physical and evidential probabilities, differ in the objectivity of their approach to data collection. Objective probability focuses on a recorded observation and its further analysis, whereas subjective probability deals with one’s judgment.
References
Franklin, J. (2015). The science of conjecture: Evidence and probability before Pascal. Baltimore, MD: Johns Hopkins University Press.
Gan, G., Ma, C., & Xie, H. (2014). Measure, probability, and mathematical finance: A problem-oriented approach. Hoboken, NJ: John Wiley & Sons.