In order to test a complaint about the low weight of seeds in packages, the null hypothesis should be made that there is no significant deviation from the declared weight standard of 50 pounds. Accordingly, at the chosen significance level α = 0.05, a test will be carried out in order to confirm or disprove the null hypothesis. Consequently, the alternative hypothesis would show that the mean is well below 50 pounds, which is what the complainant claims. The distribution areas in such a section of statistics will determine the critical value: in this case, a lower-tailed test is carried out since H1: μ < μ0. Therefore, the critical value of Z will be -1.645. The application in the general case is shown in Figure 1.
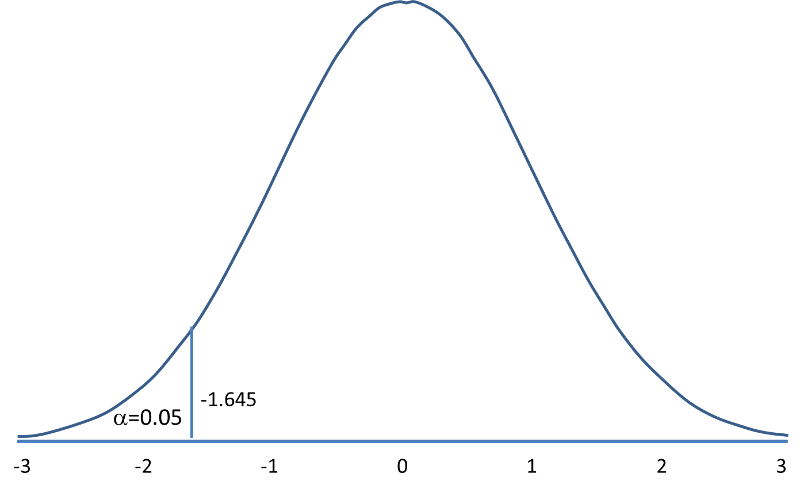
The decision rule is also determined by significance level, if not calculated by p-value. In this case, there are values -1.96 and 1.96, and if the test statistic is lower or higher than the specified values, respectively, then the null hypothesis can be refuted. The standard deviation for this formula was calculated for the sample since it was not given to the general population. The formula below is used to calculate the test statistic.
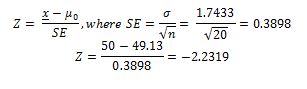
SE stands for standard error, which is found by dividing the standard deviation by the square root of the number of items in the sample. The calculated test statistic showed a value of -2.2319, less than the declared -1.96, giving the right to reject the null hypothesis and accept the alternative one. Therefore, the farmer does not fill the bags with seeds enough, and the significant deviation is what the client was talking about. However, before recalibrating the equipment, a similar test should be carried out on more packages to better verify the need for such costs.
Reference
LaMorte, W. W. (2018). Hypothesis Testing: Upper-, Lower, and Two-Tailed Tests. Web.