Mathematical sciences quite accurately describe phenomena and patterns common in everyday life. In other words, even outside of mathematics textbooks and theorems, mathematical figures, formulas, or properties studied earlier can be detected. Such statements are also true for conic sections, which form a whole range of different planar figures. Thus, depending on the location and angle used for the section, a cone can generate a circle, ellipse, parabola, or hyperbola. This paper confirms that parabolic shapes are very common in real life, which is illustrated by the example of the McDonald’s fast-food chain logo.

In fact, parabolas as one of the forms of the conic section can be found in examples from real life. For example, the letter “M” in the classic fast-food chain logo is a textbook example of two parabolas pointing downward (Artis, 2016). Thus, the standard parabola equation is written as in Equation 1. To make the parabola be inverted with respect to the abscissa axis, it is sufficient to put a minus in front of the main coefficient of the equation.
y = ax² + bx + c (equation 1)
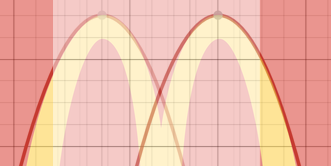
It is fair to admit that many of life’s examples of parabolas are not actually parabolas, although they are very similar. In the case of the McDonald’s logo, one can be absolutely certain that the letter “M” is described by parabolic equations because a critical analysis can be made. According to Artis, the parabola equation of the logo is given by Equation 2. By plotting the graph of this function and correlating it to the logo (Figure 2), a natural conclusion can be drawn that the function accurately describes the outer boundaries of the letter “M.” Thus, the classical version of the McDonald’s logo is indeed described by the parabolic equations, which are the shape of a conic section.
y = – x² + 8x – 11 (equation 2)
Reference
Artis, T. (2016). McDonald’s. Math With Burke.