Probability Theory
In mathematics, probability theory is used as a vast field that studies the laws associated with random events. There are no unequivocal views as to when precisely the foundations of probability theory came into being. According to one version, it originated thousands of years ago when censuses were conducted; from this paradigm, probability has sociological origins (Porter, 2022). From another point of view, probability theory is thought to have been solidified in the seventeenth century in an attempt to study gambling. The leading names in this history are the Frenchmen Pierre de Fermat and Blaise Pascal. Both Pascal and de Fermat attempted to solve the problem of the Chevalier de Mairet, who asked about a fair division of bets for two players in the event that the game was interrupted. Both researchers formulated the essential vision of modern probability theory in an attempt to find a solution.
In probability theory, the prevailing principle is the actual probability of the occurrence of a random event. To calculate this probability, a formula is used in which the number of successful cases is divided by the total number of trials. For example, if a coin was tossed fifty times and only twenty of them produced tails, then the probability of tails was 0.4 or 40 percent. The advantage of this principle is the relative simplicity of calculating the probability of a random event occurring. Among other things, it can be used to calculate the probabilities of two events at once, sequential or parallel, as well as to calculate the inverse probability. However, the probability should not be taken literally, which is its main disadvantage. For example, a tails probability of 40% does not mean that in a hundred trials, precisely 40 of them will be tails. At the same time, if an event has a 50% chance of happening, such as the probability of winning the lottery, that does not mean that of the two tickets purchased, the second will necessarily be the winning one. In other words, the main drawback of probability theory is the need for a deep understanding of the principle in order to calculate and interpret it correctly.
The Fundamental Nature of Probability
In probability theory research, there are two diametrically opposed approaches to understanding what probability really is. The first, the objective one, is based purely on actual observations and does not use assumptions (Kenton, 2022). For example, the calculations of the probability of tails or winning the lottery in the last paragraph are examples of objective probability because it is based on facts and numbers. In contrast, the subjective probability is based on personal experience and unscientific assumptions (Kenton, 2022). An example of this paradigm is, for example, an individual’s personal belief that he or she does not get into a traffic accident because he or she has not been in one before; that is, the individual believes this probability is zero. Or, for example, an individual has noticed that a public company’s stock has been rising for the past two days, so he expects its probability of rising on the third day to be high, although in a dynamic market, this need not necessarily be the case.
Calculations
The probability that a randomly selected American has never had an HIV test is:
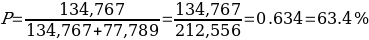
Accordingly, the probability that a randomly selected American in the sample of 212,556 has never been tested for HIV is 63.4%. It is worth clarifying that the conclusions only work for the sample because no statistical test was performed to extrapolate the results to the general population. At the same time, the proportion of Americans aged 18 to 44 who have never been tested:
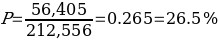
That is, there is a possibility that 26.5% of 212,556 Americans were between the ages of 18 and 44 and had never had a diagnostic test.
References
Kenton, W. (2022). Objective probability definition. Investopedia. Web.
Porter, T. M. (2022). Probability and statistics. Britannica. Web.