Introduction
One of the fundamental beginnings of mathematics is the possibility of theoretical generalization and the search for analogies between concepts, which allows various parts of mathematical disciplines to be linked together. It is necessary to understand that the development of mathematics has taken millennia and has always gone on complicating the available knowledge: from simple arithmetic counting for agricultural purposes of the first people to quantum calculations of modern mathematics. The complication of initial concepts is not always based on the deductive approach popular among researchers but can be realized through induction, as was the case with Pythagoras’ theorem. The thesis statement is that Pythagoras’ theorem, although an original concept, is only a particular case of the cosine theorem since it contains the same ideas, only in a truncated form, and allows one to determine the side of any, not necessarily a right triangle. This essay aims to develop this thesis and prove it.
Pythagoras’ Theorem: Multiple History
The common view of plagiarism among mathematical theorems can rightly be extrapolated to the case of the ancient Greek mathematician Pythagoras. In the sixth century B.C., Pythagoras was developing the previously known concepts of triples in right triangles, such values of the sides that would satisfy the provision of Pythagoras’ theorem known to the modern reader. The use of the root of the sum of the squares of the two cathetuses was noticed as early as four thousand years ago on ancient Babylonian tablets, but they were not so widely used until Pythagoras generalized them and created an equation that would solve a right triangle (Kasprik and Barros 4). It is unlikely, however, that Pythagoras independently attributed his own name to the equation he generalized; there is no definitive evidence of this. Nevertheless, there are a sufficient number of historical records, including those on behalf of ancient Greek thinkers, which report Pythagoras as the author of this concept. It is known that Pythagoras, as part of his research, visited the territory of ancient Egypt, whose inhabitants had already been using the concepts of the Egyptian triangle with sides 3, 4, and 5 several hundred years before Pythagoras’ birth (Aboulfotouh 15). After his return, Pythagoras founded his own mathematical school and began to teach knowledge, the results of which have been attributed to the name of the ancient Greek (Gregersen). Thus, it is not known for sure whether Pythagoras was the real author of this theorem or whether he had nothing to do with it at all.
What is known with certainty is that Pythagoras did not use trigonometric relations to solve right triangles. The first references, and hence the use of cosines, sines, and tangents, were not proposed until the sixth century, that is, nearly a thousand years after Pythagoras’ death (Merlet 2). In other words, the ancient Greek explorer certainly could not have used trigonometric functions in the modern sense to solve right triangles. On this basis, it is natural to assume that Pythagoras created a theorem that should be considered unique and paramount, and over time superstructures, including the cosine theorem, began to be added to it. Precisely the opposite happened — the theorem created by Pythagoras was not a generalizing theorem but rather only a particular case of the cosine theorem, which can be proved mathematically.
Pythagoras’ Theorem: A Mathematical Description
According to the classical interpretation of Pythagoras’ theorem, the hypothesis of a triangle can be calculated as the root of the sum of the squares of the two cathetuses, as shown in equation (1). For a side to be called the hypotenuse, at least two conditions must be satisfied. First, it must be the longest side of a rectangular side, and second, that side must lie opposite an angle of 90°; only when these two conditions are satisfied can the side be called the hypotenuse and can be calculated by Pythagoras’ theorem (1). Remarkably, Pythagoras’ theorem can be applied to any type of right triangle, regardless of the lengths of the cathetuses and hypotenuse. There are no restrictions on integer values either: that is, for any two cathetuses in a right triangle, it is possible to determine the values of their hypotenuse, even if this is not an integer. For example, if one uses (1) for calculations, then for a triangle with sides √2 and sides √8, opposite the angle of 90°, the hypotenuse is √10.
c = √a² + b² (1)
It is true that Pythagoras’ theorem can be used in other ways as well, for example, to determine the value of the cathetus when at least one value of the cathetus and hypotenuse is known. In this case, equation (1) is transformed into equation (2). Strictly speaking, the root of equation (2.2) should also be a negative value of the square root — thus, for a triangle with cathetus 2 and hypotenuse 4, the value of the second cathetus can be either 2√3 or -2√3. However, logically it is clear that there are no negative lengths in geometry, and for this reason, negative roots are traditionally omitted when solving the Pythagorean theorem.
c² = a² + b² (2)
→ c² – b² = a² (2.1)
→ ±√c² – b² = a (2.2)
The Cosine Law
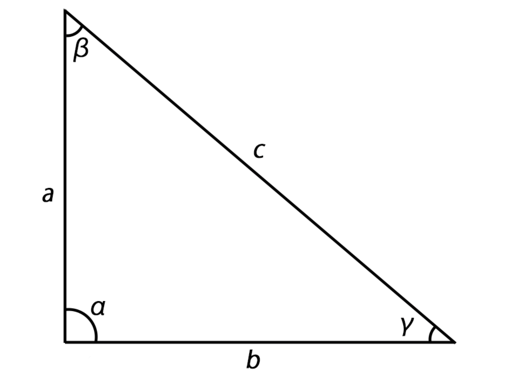
While Pythagoras’ theorem was created by Pythagoras in the sixth century B.C., the theorem or law of cosines was not developed until nearly 2,200 years later. The law of cosines is attributed to the Indian mathematician Jamshid al-Kashi, who used the triangular form of notation to solve any flat triangle, not just rectangular triangles (Berisha and Klinaku 383). Equation (3) shows the mathematical notation of this law: to calculate any of the sides, it is necessary to know the value of the other two sides and the angle α between them. The triangle depicted in Figure 1 is not necessarily a right-angled triangle and can be represented by any flat triangle at all, from an acute-angled to an obtuse-angled triangle. Regardless of the type of triangle, the law of cosines can be applied to it to calculate the unknown side. For example, as shown in equations (4)-(4.4), for a triangle with two sides, 2 and 2, and an angle between them of 35°, the third side is smaller and is 1.203. The concept of hypotenuse and cathetuses no longer applies in this case since the triangle is not rectangular.
c² = a² + b² – 2*a*b*cosα (3)
c² = 2² +2² + 2*2*2*cos35° (4)
→ c² = 4 + 4 – 8 *cos35° (4.1)
→ c² = 8 – 8 *cos35° (4.2)
→ c² = 1.447 (4.3)
c = 1.203 (4.4)
It is noteworthy that the cosine theorem can also be applied to find an unknown angle, but in this case, as follows from equation (3), it is necessary to know all three sides of the triangle. For example, as shown in equation (5)-(5.6), for a triangle with sides 3, 5, and 3, the angle between sides 3 and 3 is 112.9° since the remaining roots of the trigonometric equation do not satisfy the condition of 180° equality of all three angles within the triangle.
5² = 3² + ²3 -2*3*3*cosx (5)
→25 = 9 + 9 – 18*cosx (5.1)
→25 = 18 – 18*cosx (5.2)
→7 = – 18*cosx (5.3)
→7/- 18 = cosx (5.4)
→x = cos¯¹ (-7/18) (5.5)
→x = 112.9° (5.6)
Relationship between the Pythagorean Theorem and the Law of Cosines
As shown above, Pythagoras’ theorem is used to calculate any side of a right triangle, while the cosine theorem is used to calculate sides or angles in any triangle at all. Thus, the scope of both mathematical concepts is the first evidence of the generalizable nature of the law of cosines. However, this relationship can be looked at differently: in a right triangle, the angle between the two cathetuses is always 90°. It is known that the cosine of this angle is zero, which means that in the formulation of the cosine theorem, the third term of the sum is zero. Thus, as shown in equations (6)-(6.2), with a right angle between the sides, the cosine theorem takes the form of the Pythagorean theorem. In other words, the Pythagorean theorem is really a particular case of the more generalized law of cosines, despite the significant age difference between the two concepts.
c² = a²+ b² – 2*a*b*cos90° (6)
c² = a²+ b² – 2*a*b*0 (6.1)
c² = a²+ b² (6.2)
Similar math work for vector calculus on the coordinate plane. According to the definition, the difference between two vectors defined by the third side of a triangle is equal to the root of the sum of the squares of these vectors minus the doubled value of their product by the cosine of the angle between them, as shown in equation (7). However, if the angle between two vectors is straight, the cosine again becomes zero, which leads to the formulation of the Pythagorean theorem in vector form as shown in (7.1), which again confirms the related connection between the theorems.
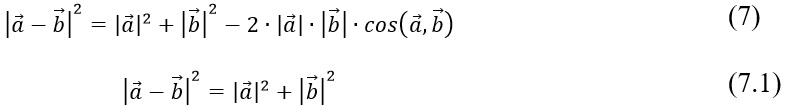
Conclusion
To summarize, although Pythagoras’ theorem is an original concept from presumably ancient Greek mathematics, it is only a particular case of the more modern law of cosines. The essay showed that the Pythagorean theorem has several restrictions related to the necessity of a right angle between the cathetuses, whereas the cosine theorem has no such restrictions. Thus, Pythagoras’ theorem applies only to right triangles, while the law of cosines can be used to solve any flat triangles at all. The connection between the two concepts is based on a generalization: in the case where the angle between two sides is 90°, the law of cosines turns into the Pythagorean theorem.
Works Cited
Aboulfotouh, Hossam. “Using the Triangle 6-8-10 in Land Survey Problems in Rhind Mathematical Papyrus.” Scientific Culture, vol. 5, no. 3, 2019, pp. 13-17.
Berisha, Valbone, and Shukri Klinaku. “The Law of Cosines and the Lorentz Factor.” Physics Essays, vol. 31, no. 4, 2018, pp. 383-386.
Gregersen, Erik “Pythagorean Theorem.” Britannica, 2020.
Kasprik, L. A., and A. C. Barros. “Ancient Mesopotamian’s System of Measurement: Possible Applications in Mathematics and Physics Teaching.” Journal of Physics: Conference Series, vol. 1512, no. 1, 2020, pp. 1-10.
Merlet, Jean-Pierre. “A Note on the History of Trigonometric Functions and Substitutions.” Proceedings of HMM.