Introduction
Transport models are useful in cost limitation (Anderson, Sweeney, Williams, Camm, Martin, 2010). The shipping and transportation model proposed in this paper aims to limit the costs incurred in the transportation of wastes from various plants (per week). The model ensures that only the cheapest options are included. Consideration of the plants holding capacity is included.
The amount of waste generated every week is within the table below:
The cost of shipping a barrel of waste to each of the waste sites is summarized in the table below:
The following tables give the estimated shipping costs per barrel across the plants.
Plant
The estimated shipping cost per barrel between each of the three waste disposal sites is as follows:
Waste Disposal Site
The model solutions illustrate the outcome of the developed shipping schedule and provide evidence for its adoption. It proposes a minimal cost schedule. Assuming that the number of waste barrels shipped from a given site i to another site, denoted by the expression xij , then the total cost of transportation should be as follows:
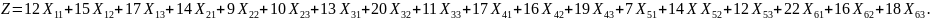
The function defines the proposed model seeking to minimize transportation costs (Buglear, 2005). While attempting to minimize transportation costs, the model takes into consideration resource constraints as indicated by the equations below:
Plant availability
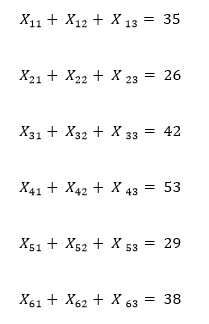
Site holding capacity
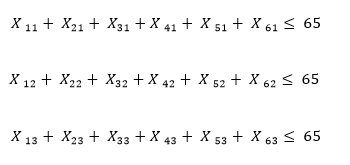
i and j are non-negative and represented by the expression below:
Xij≥0, i=1,2,3,4,5,6; j=1,2,3.
Based on the linear model developed and constraints described, an excel spreadsheet is used to aid evaluation. The excel sheet is attached.
In the model, the cheap routes are preferred. The constraints highlighted earlier are taken into consideration to ensure that wastes beyond a site’s capacity are not allocated to it, and similarly, plant availability is not exceeded in planning. The final calculation is then based on the model
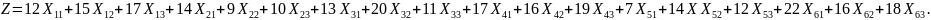
The resulting model’s results are in the tables below:
Discussion
From the results, Whitewater and Los Canos should receive wastes to their maximum capacity given that the associated shipment costs are lesser than Duras. The remaining waste load is disposed to Duras whose capacity is non-exploited. Plants offering reduced cost are preferred. Danville, Macon, and Columbus plants are used. The decision to use the sites is based on the costs associated with waste processing. All the wastes from Columbus will be disposed to Whitewater, while those from Danville will be disposed to Los Canos. Finally, wastes from Macon will be disposed of at the Duras site. These decisions are based on the cheapest transportation costs from the respective plants to the mentioned disposal sites. Based on the model, a total cost of $2630 is spent in disposing of all the wastes generated.
Limits of study
Development of the model is limited by the fact that its results are only estimates and do not take into consideration future possibilities including economic projections, transport forecasts, region attractiveness, demographics among others (Buglear, 2005).
References
Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., Martin, R. K. (2010). Quantitative methods for business. (11th Ed.) Mason, OH: South-western (Cengage).
Buglear, J. (2005). Quantitative methods for business: the A to Z. Oxford, U.K.: Elsevier Butterworth-Heinemann.