In regression analysis, the relationship between dependent and independent variables is the focus of all calculations. The quality of all measurements and their connections have to be checked to ensure that the results of a research show correct results. To achieve this goal, such measures as the coefficient of determination are used. According to Chicco et al. (2020), the coefficient of determination is “the proportion of the variance in the dependent variable that is predictable from the independent variables” (p. e623). This definition describes this calculation as a connection between dependent and independent variables, thus checking the data’s quality.
As shown in the description of the term, the coefficient of determination, written simply as R2, determines whether independent variables affect dependent variables in a consistent way. The formula for calculating R2 is:
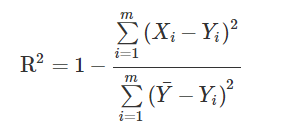
One can see that the measurement compares the mean square error and the mean total sum of squares (Chicco et al., 2020). By dividing one by the other, one can see what portion of the variation is covered by the change in independent variables.
In regression analysis, R2 is used to show whether the chosen type of regression model is an appropriate fit for the study. This implies that the coefficient is used to determine the significance of the whole equation presented to prove the hypothesis. As regression analysis uses a linear connection between the variables, R2 is vital for determining if the presented formula is close to the results obtained from raw data (Baždarić et al., 2021). The significance shown by the coefficient is demonstrated with a number between 1 and 0.
If the coefficient is large, this implies a minimal deviation of cases from the linear regression. In turn, the lack of difference between the two calculations signifies that the regression accurately predicts the connection between dependent and independent variables and that the final conclusions are consistent with the collected information. In contrast, if R2 is close to 0, the variation of errors is considerable, and the chosen regression model is not representative of the data (Chicco et al., 2020). It cannot adequately explain the margin of error and the relationship between variables for the proposed hypothesis and thus cannot be viewed as significant.
As with many other types of statistical calculations, the coefficient of determination is affected by sample size. A small sample suggests that the results’ mean is likely to be affected by outliers and cases that differ from the rest of the sample significantly (Xu et al., 2022). In contrast, a large sample size helps the researcher to pinpoint which individual cases differ greatly from the rest. Therefore, a small sample lowers the quality of data as a whole, and it affects the results of such calculations as R2 (Xu et al., 2022). It should also be noted that the coefficient is calculated by comparing sums of errors and changes in the variables’ position. Therefore, it is vital to collect enough data to identify a pattern for the regression and consider it viable.
To conclude, the coefficient of determination (R2) is essential for research that utilizes regression analysis. This measurement is used to determine the fit of the used linear regression, and it checks the relationship between dependent and independent variables. Large R2 is usually indicative of high significance, allowing one to see a clear connection between selected variables. However, sample size impacts the outcome of the analysis, and a large number of participants or data sets is crucial for increasing the quality of R2 results and the quality of research in general.
References
Baždarić, K., Šverko, D., Salarić, I., Martinović, A., & Lucijanić, M. (2021). The ABC of linear regression analysis: What every author and editor should know. European Science Editing, 47, 1-9. Web.
Chicco, D., Warrens, M. J., & Jurman, G. (2021). The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Computer Science, 7, e623. Web.
Xu, X., Du, H., & Lian, Z. (2022). Discussion on regression analysis with small determination coefficient in human‐environment researches. Indoor Air, 32(10), e13117. Web.