The fundamental theoretical construct of information gain and entropy is the foundation of data science. This paper aims to describe its applications and limitations to data analysis.
Uses and Examples
The first type of application may be regarded as a method of assessing probability in the form of forecasts for point processes. The entropy rating of an observed result with a probability forecast of p is –log p (Fan et al., 2011). If p is produced from a probabilistic model, then there is a baseline model with probability for the same event (Fan et al., 2011). Then, the log proportion log(p/) is the likelihood gain, and its predicted value is the information gain for that result (Fan et al., 2011). The probability of the system and its entropy rate are both strongly linked notions (Daley and Vere-Jones, 2005). When the results in consideration are the frequency or probability of failure of episodes in a randomized point process, the linkages between these notions are investigated (Buscemi, Das and Wilde, 2017). The mean data augmentation per unit time, forecasting made at configurable discrete points in time, is bounded above the entropy ratio of the set of points in this context (Yin and Xi, 2017). As a result, the above information represents one of the methodology’s potential applications.
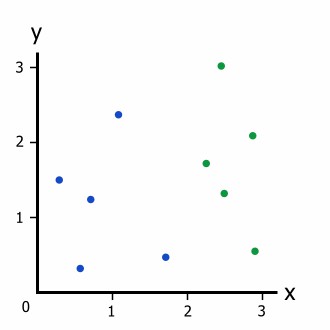
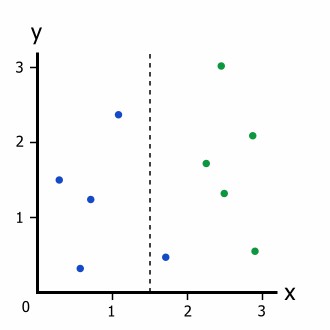
Information Gain, similar to Gini Impurity, is a tree-based training metric. These metrics precisely assess the quality of a split shown on Figure 2. For instance, if anyone has the data in Figure 1, it is interesting to think about what would happen if the data were split at x = 1.5. Figure 2 shows that the split is incomplete, with four blue dots on the left and one blue and five green dots on the right branches. Nevertheless, there is no established method for determining the degree to which the split is efficient (Kozak, Kania and Juszczuk, 2020). Thus, to quantify the kind of a split, it is required to use information gain and entropy; the example mentioned above demonstrates the use of Gini Impurity and splits classification.
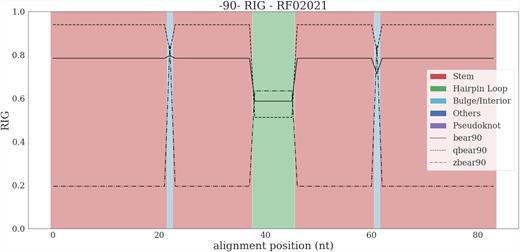
The pre-miRNA family RF02021, also known as mir-3179, has a capsid structure with a core hairpin loop that varies in size. The short internal loop is also changeable, but one can deduce from the substitution scores that it is frequently swapped with more favorable structural contexts (Figure 3). There are several scenarios: zBEAR has better RIG scores than a complete alphabet due to a coarser encoding (Pietrosanto et al., 2021). In the basic level of abstraction, the fundamental alignments have a set of preserved places (Pietrosanto et al., 2021). For example, in a stem context, nucleotides occupy such locations, but the finer-level features are not favorable in terms of replacement (Oladyshkin and Nowak, 2019). As a result, several stem lengths are aligned, although the proportions of the branches involved are rarely encountered together.
The structuring contexts are not preserved when low RIG scores are associated with sized particles compression algorithms, and high values are associated with fine-grained encodings. Such sites involve numerous distinct contexts, such as internal loops, stems, and hairpin loops, although their replacement rating at a higher degree of specificity is acceptable (Reddy and Chittineni, 2021). When various hairpin lengths are involved, this can be the condition for the 5′ hairpin structure, which can be matched with the 3′ of the equivalent 5′ stem (Crevecoeur, 2019). Consequently, this particular example explains how data augmentation and entropy are used in two directions: RNA analysis and RIG scores.
Several inequalities limit how successfully scientists can handle physical systems to reach any desired aim in physics. The entropy, the second law of thermodynamics, limitations in quantum communication theory, and the perturbation theory of quantum mechanics are examples (Rychtáriková et al., 2016). Recent published scientific findings have improved these limiting assertions physically, influencing how successfully one may attempt to remediate an irreversible process (Nowozin, 2012). Implementing and extending these results makes it feasible to produce considerable enhancements to numerous entropy inequalities, such as entropic disturbance, information gain, entropy gain, and complete positivity of nonlinear dynamical systems dynamics (Nowozin, 2012). The immediate result in this situation is a residual term for a quantum channel’s entropy increase (Chicharro and Panzeri, 2017). As a result, adopting the suggested data analysis methods benefits the research mentioned above.
Limitations and Inaccuracies
However, employing information gain and entropy has drawbacks and limitations. When examining circumstances, the information gained has always been slanted upward (Otte et al., 2017). It commonly happens when two items collide: one has a small sample and numerous variable levels that are not computed evenly, while the other has a large sample (Otte et al., 2017). In most cases, the reason is that, in most cases, naïve information gain or a sample estimate is obtained (Provost and Fawcett, 2013). As a result, differences in observed probabilities from theoretical will, with a high probability, impact it. The observed likelihood deviations will be exaggerated if fewer observations compound more variable levels. These conclusions show two significant flaws: sample bias and identifying circumstances.
Additionally, there is a limitation which mostly affects the entropy rather than the information gain, though they are coherent in this particular case. There is a constraint that mostly effects entropy rather than information gain, but the two are related in this situation (Müller, 2020). The combination of the system’s entropy and its surroundings changes, S sys + S sur, can only be larger than or equal to zero for any process (Müller, 2020). There will never be a reduction in the entropy of the cosmos (Müller, 2020). As time passes, S iso = S sys + S sur 0 is going to occur (Müller, 2020). Thus, the theoretical inability of calculating cases which are linked to the negative spectrum limit the possible analysis opportunities.
Reference List
Buscemi, F., Das, S., and Wilde, M. M. (2017) ‘Approximate reversibility in the context of entropy gain, information gain, and complete positivity’, Physical Review A, 93(6), 062314. Web.
Chicharro, D., and Panzeri, S. (2017) ‘Synergy and redundancy in dual decompositions of mutual information gain and information loss’, Entropy, 19(2), 71. Web.
Crevecoeur, G. U. (2019) ‘Entropy growth and information gain in operating organized systems’, AIP Advances, 9(12), 125041.
Daley, D. J., and Vere-Jones, D. (2005) ‘Scoring probability forecasts for point processes: the entropy score and information gain’, Journal of Applied Probability, 41(A), 297-312.
Fan, R. et al. (2011) ‘Entropy‐based information gain approaches to detect and to characterize gene‐gene and gene‐environment interactions/correlations of complex diseases.’ Genetic epidemiology, 35(7), 706-721.
Kozak, J., Kania, K., and Juszczuk, P. (2020) ‘Permutation entropy as a measure of information gain/loss in the different symbolic descriptions of financial data’, Entropy, 22(3), 330. Web.
Müller, J. G. (2020) ‘Photon detection as a process of information gain’, Entropy, 22(4), 392. Web.
Nowozin, S. (2012) ‘Improved information gain estimates for decision tree induction’, arXiv, 1206.4620. Web.
Oladyshkin, S., and Nowak, W. (2019). ‘The connection between Bayesian inference and information theory for model selection, information gain and experimental design’, Entropy, 21(11), 1081.
Otte, et al. (2017) ‘Entropy-based strategies for physical exploration of the environment’s degrees of freedom’, IEEE/RSJ, pp. 615-622.
Pietrosanto, M. et al. (2021) ‘Relative information gain: Shannon entropy-based measure of the relative structural conservation in RNA alignments’, NAR genomics and bioinformatics, 3(1), lqab007. Web.
Provost, F., and Fawcett, T. (2013) Data Science for Business: what you need to know about data mining and data-analytic thinking. O’Reilly Media, Inc.
Reddy, G. S., and Chittineni, S. (2021) ‘Entropy based C4. 5-SHO algorithm with information gain optimization in data mining’. PeerJ Computer Science, 7, e424. Web.
Rychtáriková, R. et al. (2016) ‘Point information gain and multidimensional data analysis’, Entropy, 18(10), 372. Web.
Yin, C., and Xi, J. (2017) ‘Maximum entropy model for mobile text classification in cloud computing using improved information gain algorithm’, Multimedia Tools and Applications, 76(16), 16875-16891. Web.