Introduction
As a definition, regression analysis is a statistical tool that is used to develop and approximate linear relationships among various variables. Regression analysis formulates an association between several variables. When coming up with the model, it is necessary to separate between dependent and independent variables. The model generated is used to explain the effects of the independent variables on the dependent variable. For instance, how changes on the independent variable affects the dependent variable. Further, regression can either be simple (makes use of one explanatory variable) or multiple (makes use of several explanatory variable). In most cases, analysts use regression models to predict trends of future variables.
Purpose and objectives
The paper seeks to develop a linear demand equation. The regression will be carried out of quantity demanded on the price of the commodity, the price of related good, income and advertising from 1980 to 2011. The regression analysis will be carried out in linear form and log linear form. Further, the paper will compute various point elasticities of demand and interpret the results generated. Finally, test of significance will be carried out on the variables used in the linear and log linear model of the regression line.
The linear demand equation
This section will focus on formulating the linear regression model of demand of the commodity. It concentrates on computing the various point elasticities of demand and interpretation of the results. Finally, it will discuss the usefulness of elasticities in the business decision making process.
Multiple linear regression model
As mentioned earlier, when more than one factor is used when coming up with the regression equation, then a multiple regression analysis will be used. There are a number of factors that affect the demand of a product. Some of the factors are price of the commodity, competition, news about the company, and amount spent on advertising among other factors. When coming up with the simple linear regression model, it is necessary to separate between dependent and independent variables. In the analysis, the dependent variable is the demand of the product while the while the independent variables are the price of the product, the price of related good, income, and advertising. The regression line will take the form
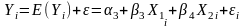
when the ordinary least squares method is used. The regression line can be simplified as shown below.
Simplified regression equation Y = b0 + b1X1 + b2X2 + b3X3 + b4X4
- Y = Demand of the commodity
- X1 = Price of the commodity
- X2 = Price of related good
- X3 = Income
- X4 = Advertising
The theoretical expectations are b0, b2, and b4 can take any value, b1 < 0 (negative) while b3 > 0 (positive).
The data
The table presented below shows the complete data for quantity of the good demanded, the price of the commodity, the price of the related good, income and advertising to be used in subsequent calculations and analysis.
Regression results
The table presented below shows the results of the regression analysis.
From the above table, the regression equation can be written as Y = 434.6470 – 1.2207X1 – 0.1227X2 + 0.000021972X3 – 0.0027X4. The intercept value of 434.6470 represents other variables that affect the demand of the commodity but are not included in the model. The coefficient value of 1.2207 implies that if the price of the commodity increases by one unit, the quantity demanded will decline by 1.22. The coefficient value of 0.1227 implies that if the price of the related good increases by one unit, the quantity demanded will decline by 0.1227. The coefficient value of 0.000021972 implies that if income increases by one unit, the quantity demanded will increase by 0.000021972. Finally, the coefficient value of 0.0027 implies that if the advertising expenditure increases by one unit, the quantity demanded will decline by 0.0027.
Elasticity
Elasticity measures how the quantity demanded will change when there are changes in market conditions. Point elasticity of demand is calculated using values at a particular point and not the difference between the start and the end period. Elasticity as a measure depends on how well a market condition is defined. Goods will tend to be elastic in a more narrowly defined market.
The table presented below shows the estimates for 2012 that will be used for analysis.
From the values presented in the table above, the quantity demanded of the commodity for the year 2012 can be estimated as shown below.
- Y = 434.6470 – 1.2207X1 – 0.1227X2 + 2.1972X3 – 0.0027X4
- Y = 434.6470 – 1.2207 (233.75) – 0.1227 (269.5) + 0.00002.1972 (4395255.48) – 0.0027 (1007.6)
- Y = 210.09.
Therefore, the estimated demand for the year 2012 is 210.09.
Price elasticity of demand
Price elasticity of demand is a measure how the quantity demanded of a good change when the price of the commodity changes. However, this measure of elasticity of demand of a commodity is subject to some inadequacies. First, it ignores the presence of other related goods in the market such as close substitutes and compliments as changes in prices or demand of these goods would affect the elasticity of the good in question. It also ignores the type of product in question since necessities and luxuries would have different elasticities. Demand for luxuries do not respond to changes in price. In addition, this measure overlooks time horizons. Goods tend to be more elastic over a longer period of time. The computation of point – price elasticity of demand for the commodity is presented below.
Point – price elasticity = Percentage change in quantity demanded
Percentage change in price of the commodity = (210.09 – 234.5) / 234.5 = -0.10409 / 0.1 = -1.040
The elasticity implies the commodity is elastic since the coefficient of elasticity is slightly greater than 1.
Cross price elasticity of demand
It is a measure of degree of response to changes in quantity demanded of a good as a result of a change in the price of related good. This type of measure of elasticity gives information on whether two particular commodities are complementary or substitutes. The computation of point – cross price elasticity of demand for the commodity is presented below.
Point – cross price elasticity = Percentage change in quantity demanded of good Y
Percentage change in price of the good X = -0.10409 / 0.1 = -1.0409
The negative value implies that the two goods are complimentary. That is, they are used together.
Income elasticity of demand
Income elasticity of demand measures the degree of response of changes in quantity demanded of a commodity to changes in the income of an individual. This type of measure of elasticity gives information on the nature of a commodity. Based on this measure, a commodity can either be luxury or inferior. The computation of point – income elasticity of demand for the commodity is presented below.
Point – income elasticity = Percentage change in quantity demanded of the commodity
Percentage change in income = -0.10409 / 0.1 = -1.0409
The negative sign implies that the elasticity represents an inferior good. That is, as the income of the individual increases, the quantity demanded declines.
Advertising elasticity of demand
Advertising elasticity of demand measures the degree of response of changes in quantity demanded of a commodity to changes in the amount spent on advertisement. This type of measure of elasticity gives information on how the volume of quantity demanded of a commodity will respond to changes in advertisement expenditure. The computation of point – advertising elasticity of demand for the commodity is presented below.
Point – advertising elasticity = Percentage change in quantity demanded
Percentage change in advertising expenses = -0.10409 / 0.1 = -1.0409
The coefficient of -1.0409 implies that demand will respond negatively to an increase in advertising. This can be an indication that the product has passed the maturity stage in the market and its losing market share to its competitors.
Use of elasticity in decision making process
As mentioned earlier, elasticity of demand estimates the degree to which sales volume when various variables such as the price of the commodity, the price of related commodities, income, and advertisement among other variables change. These measures are quite significant in the decision making process of a business. To start with, the concept of elasticity advises business owners of the types of products to supply in various markets. For instance the uptake of certain products is highly affected by income elasticity. Thus, a population with a certain income elasticity may not purchase certain category of products. Secondly, the concept of elasticity helps businesses understand the categories of customers. Thus, a company may focus on producing commodities that target a given group of customers. For instance, consumers with high income and high income elasticity are likely to be less responsive to changes in prices. Such a group of customers is suitable for introducing a new product in the market. Thus, by understanding the customer group, the business owners are in a good position for the product to offer to various groups of customers.
Further, the concept of elasticity helps in the management of the life cycle of a product. Thus, businesses will know when they are facing stiff competition from substitute product. This guide them on knowing the age of a product in the market. This information is vital in controlling the volume of production. Also, the concept of elasticity helps firms in choosing an appropriate pricing strategy to use in a give market. The concept is known as price discrimination. This decision is highly determined by the price elasticity of the commodity. This also aids management is estimating total revenue. Further, the concept of elasticity also aids management in determining the goods tax. Finally, elasticity of demand in relation to expenses relating to sales helps business to know how sales volume will respond when there are changes in such expenses. Thus, expenses which are likely to cause an increase in sales volume are likely to be increased because they contribute positively to the profitability of the business.
The demand equation in log-linear form
This section will focus on formulating the log – linear regression model of demand of the commodity. It also concentrates on computing the various point elasticities of demand based on linear variables and interpretation of the results.
Multiple log – linear regression model
The log – linear regression line will take the form lnY = b0 + b1lnX1 + b2lnX2 + b3lnX3 + b4lnX
- lnY = Demand of the commodity
- lnX1 = Price of the commodity
- lnX2 = Price of related good
- lnX3 = Income
- lnX4 = Advertising
The theoretical expectations are b0, b2, and b4 can take any value, b1 < 0 (negative) while b3 > 0 (positive).
The data
The table presented below shows the complete data for quantity of the good demanded, the price of the commodity, the price of the related good, income and advertising transformed to logarithmic form.
Regression results
The table presented below shows the results of the regression analysis.
From the above table, the regression equation can be written as Y = 4.0606 – 1.6671X1 – 0.1184X2 + 0.3862X3 – 0.0265X4. The intercept value of 4.0606 represents other variables that affect the demand of the commodity but are not included in the model. The coefficient value of 1.6671 implies that if the price of the commodity increases by one unit, the quantity demanded will decline by 1.6671. The coefficient value of 0.1184 implies that if the price of the related good increases by one unit, the quantity demanded will decline by 0.1184. The coefficient value of 0.3862 implies that if income increases by one unit, the quantity demanded will increase by 0.3862. Finally, the coefficient value of 0.0265 implies that if the advertising expenditure increases by one unit, the quantity demanded will decline by 0.0265.
Elasticity
The table presented below shows the estimates for 2012 that will be used for the calculations.
From the values presented in the table above, the quantity demanded of the commodity for the year 2012 can be estimated as shown below.
- Y = 4.0606 – 1.6671 (2.560095) – 0.1184 (2.628083) + 0.3862 (7.261750583) – 0.0265 (3.258085021)
- Y = 2.19964942
Price elasticity of demand
The computation of point – price elasticity of demand for the commodity is presented below.
Point – price elasticity = Percentage change in quantity demanded
Percentage change in price of the commodity = (2.19964942 – 2.37014) / 2.37014 = -0.071932704 / 0.1 = -0.7193
The coefficient elasticity implies the commodity is inelastic because the value is less than one.
Cross price elasticity of demand
The computation of point – cross price elasticity of demand for the commodity is presented below.
Point – cross price elasticity = Percentage change in quantity demanded of good Y
Percentage change in price of the good X = -0.071932704 / 0.1 = -0.7193
The negative value implies that the two goods are complimentary. That is, they are used together.
Income elasticity of demand
The computation of point – income elasticity of demand for the commodity is presented below.
Point – income elasticity = Percentage change in quantity demanded of the commodity
Percentage change in income = -0.071932704 / 0.1 = -0.7193
The negative sign implies that the elasticity represents an inferior good. That is, as the income of the individual increases, the quantity demanded declines.
Advertising elasticity of demand
The computation of point – advertising elasticity of demand for the commodity is presented below.
Point – advertising elasticity = Percentage change in quantity demanded
Percentage change in advertising expenses = -0.071932704 / 0.1 = -0.7193
The coefficient of -1.0409 implies that demand will respond negatively to an increase in advertising. This can be an indication that the product has passed the maturity stage in the market and its losing market share to its competitors.
Statistical significance of explanatory variables at the 5% significance level Testing the statistical significance
Testing statistical significance shows whether the explanatory variable is a significant determinant of the demand of the commodity. A t – test will be used to test the statistical significance since the sample size is small. A two tailed t- test is carried out at 5% significance level.
Null hypothesis: Ho: bi = 0
Alternative hypothesis: Ho: bi ≠ 0
The null hypothesis implies that the variables are not significant determinants of demand. The alternative hypothesis implies that variables are significant determinant of demand.
Test of significance for the linear model
The table presented below summarizes the results of the t – tests.
Test of significance for the log linear model
The table presented below summarizes the results of the t – tests.
The results for linear and log – linear model are similar. From the two tables above, the values of t – calculated are greater than the values of t – tabulated for two variables these are, the price of the commodity and income. Therefore, the null hypothesis will be rejected and this implies that the two variables are significant determinants of demand at the 5% level of significance. Further, the values of t – calculated are less than the values of t – tabulated for two variables these are, the price of related good and advertising. The null hypothesis will be rejected and this implies that the two variables are not significant determinants of demand at the 5% significance level. The value of the intercept is not relevant when testing the significance of the regression variables.
F – test of the regression models
The overall significance of the regression model can be analyzed using an F – test. The test will be carried out 1% significance level.
Null hypothesis H0: β0 = β1 =, = βp
Alternative hypothesis H1: βj ≠ 0, for at least one value of j
The null hypothesis implies that the overall regression line is not significant. The alternative hypothesis implies that overall regression line is significant.
F – test for the linear model
The table presented below summarizes the results of F – test for the linear regression equation.
F – test for the log – linear model
The table presented below summarizes the results of F – test for the log – linear regression equation.
The results for linear and log – linear model are similar. Based on the two tables presented above, the value of F – computed is greater than the value of F – tabulated. Thus, the null hypothesis will be rejected. This implies that the overall linear and log – linear regression lines are significant.
Selection of superior model
The linear and log – linear models gives different interpretations of the results obtained. The linear model gives an interpretation of the marginal effects of the variables used. This implies that the elasticities will fluctuate depending on the data being used. On the other hand, log – linear form gives explanations as elasticities. Thus, it assumes a constant elasticity of all data set. Based on economic underpinning, when OLS is used, none of the functional model is superior to the other. Since the dependent variables used in the case of linear and log – linear form is similar, the value of R – square can be used to determine the model that is superior to the other. First, the dependent variable in the log – linear form will be converted to antilog before computing the value R – square to be used for comparison with the R – square from the linear model. The results of R – square are presented in the table shown below.
Based on the results from the table above, it can be observed that the value of R – square for log – linear form is slightly higher than that of the linear model. Thus, the log – linear form can be considered superior than the linear form and should be used for the estimation of the demand equation.