The Cournot Model Definition

Words: 1429 Pages: 5

Cournot Model of Competition

Cournot competition, also called Cournot duopoly, is an economic model of imperfect competition in which firms making homogeneous and undifferentiated products compete on the amount of the output they will produce (McAfee et al. 234). Importantly, both firms independently and simultaneously decide on the output. The Cournot model of competition makes a number of assumptions:

There is no product differentiation;
Not price but quantity is the main variable;
Firms aim at maximizing their profit and do not cooperate;
Each firm considers the output of another firm to be constant;
There is a certain number of firms in the industry;
Each firm’s output decision does not affect output decisions of its rivals;
The equilibrium concept used is the Nash equilibrium.

If only two firms compete, equilibrium in a Cournot competition is achieved at a lower price and a higher total volume of output than in a monopoly environment. To be more specific, the process will be as follows: one of the firms chooses the volume of output maximizing the company’s own profit. Then, the second firm, assuming that the level of the output of the first firm remains unchanged, determines its own output aimed at maximizing profit. This process of adjustment goes through several stages until the moment firms reach a state of equilibrium when none of them will strive to change the volume of the output.

For example, there are two firms, A and B, and Q₁ and Q₂ are the outputs produced by these firms. Let us assume that the whole output equals 100 units. Firm A predicts that the output of firm B will be 70 units and thus decides its own output to be 30 units. However, the prediction does not become a reality, and the output of firm B is 50 units. As a result, sales do not fully cover the demand since 30+50<100. If firm B produces more products than expected, for example, 90 units, there will be an excess of supply over demand. It is obvious that for the next time, both firms will correct their predictions until they reach equilibrium. The more firms operate in the industry and the higher the degree of interchangeability of their products, the greater the equilibrium in terms of Cournot competition resembles equilibrium in perfect competition.

Calculating the Profit and Outputs

In the classical Cournot theory, the demand function is:

p=a-bQ=a-b(q₁+q₂)

A is the highest possible price on the market, b is the coefficient of the inverse relationship of the quantity of the product (Q) and the corresponding price prevailing on the market. Quantity of the output produced (Q) consists of outputs of firms in the industry. Assuming that there is a model with two firms (duopoly), the best response functions should be calculated. Price function for the industry is P(q₁+q₂); cost structure of each firm is C_i q₁ Firm i profit is:

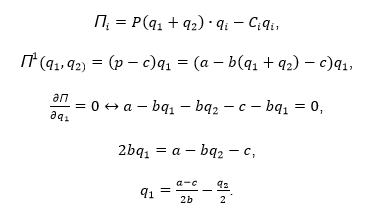
This is the reaction formula of q₁, which means that optimal quantity which firm 1 should produce considers the quantity of the second firm q₂. When solving a similar problem for firm 2, a system of equations is obtained:

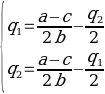
The equilibrium outputs will thus be:

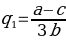
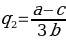
The best response is quantity q₁ that maximizes profit П₁ , given q₁ , with i ≠ j , where q₁ is the output of the opponent firm (McAfee et al. 234). Hence the best values of output are the ones that satisfy this equation. There is equilibrium when q₁ is the best response for q₂ and q₂ is the best response for q₁ . In such a case, none of the firms wants to deviate from its output level.

Perfect Competition

Perfect competition is associated with the lowest price, highest quantity, and zero profit. Therefore, perfect competition formula is: P=MR, where MR is marginal revenue. Total quantity and the equilibrium price are:

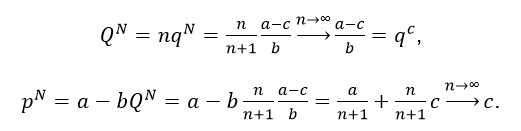
Perfect competition may be approximated by Cournot market in case there are many firms. If the number of firms in the oligopoly is going to infinity, the Nash-Cournot equilibrium makes perfect competition, as the deadweight loss is going to zero.

Advantages and Disadvantages of the Cournot Model

It should be mentioned that the Cournot model of competition has several advantages. Firstly, it thoroughly explains how two firms reach the stage of the stable Nash equilibrium. Secondly, the model gives reasonable results with prices and quantities balancing between monopolistic and competitive levels (Khoi et al. 298). Nevertheless, the theory has certain drawbacks which stem from its rather unrealistic assumptions. According to the Cournot theory, firms are considered to be absolutely equal to each other in all production and economic parameters. However, this does not correspond to reality, where the market appears to have an asymmetrical form, with one company being a leader in a particular industry and other firms being followers.

Also, the Cournot classical model assumes that two firms set quantity strategies independently of each other, which is rather unrealistic, as companies are usually responsive to strategies of their competitors. The model considers quantity to be the main variable, though, in reality, firms tend to choose prices rather than quantities. It is presumed that a product is homogenous, though it is a hard task to find homogeneity in the products offered by different suppliers.

Cournot Model: Competition Scenario

In a competitive environment, when there are several firms producing homogenous products for the market, the tariff can significantly impact the behavior of market players. Therefore, it is important to consider how both the price and the output in Cournot oligopoly change with a new tariff. In the given part of the essay, a tariff is imposed on the homogeneous product of steel. An analysis with the incorporation of the Cournot model of competition will be conducted in order to determine how the competition will affect the interaction between firms in terms of the output produced.

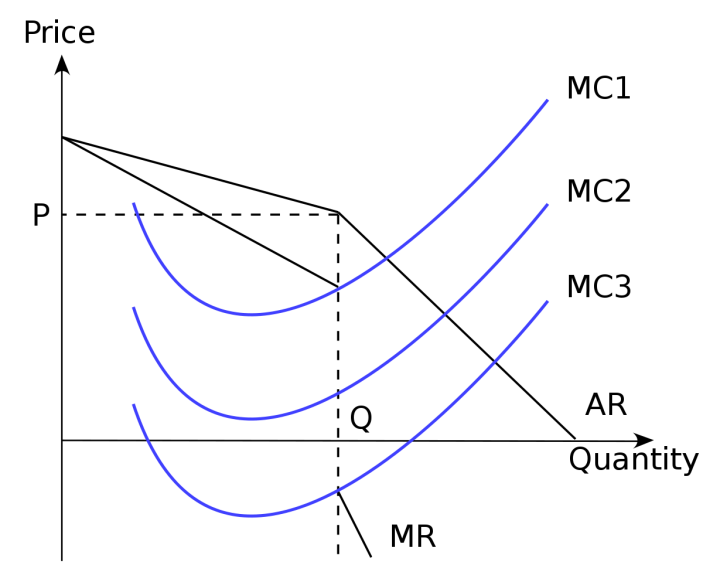
Market competition, according to the Cournot model, is characterized by each firm independently deciding on its output with a view to maximize profit. If the government imposes a tariff on every single steel product, marginal costs will increase by t, which is the value of tariff. Therefore, prices will grow with the consideration of tariff and be equal to p+t. It is found that changes in marginal cost (MC) do not influence output and prices as long as MC is in the vertical portion of MR (see fig. 1). This is in compliance with the rule that the optimal quantity of output for each firm is the one where marginal revenue equals marginal cost.

In this case, the firm will be able to obtain maximum profit. However, if the profit maximization rule is violated and the demand decreases with an increase in price, a decrease in the output produced should be expected.

*Fig. 1. The kink demand curve from (“Kinked demand”).*

Now it is important to prove that, since the products are identical and homogeneous, outputs of the firms will be equal or symmetric if the tariff introduced does not lead to profit maximization rule violation. Let us assume that there are N firms in the industry that produce steel products on which the tariff is imposed. According to the Cournot model of competition, these firms compete by simultaneously deciding on the outputs. For convenience, let us consider that all the firms have similar functions of costs c(q) = cq , where c>0. The inverse function of the aggregate demand for production of the given industry p(Q) is differentiated, and p(Q)<0 for any Q>0 and p(0)>c. It is thought that there is equilibrium in the given model.

Let us assume that in the equilibrium, outputs of the firms are different. There are two firms being analyzed, j and i, and q_j > q_i . Then: p(Q)q_j– cq_j→max, where Q= q_i+…+q_N

Considering that q_j > q^{_{i ≥}} 0, which means that q_j > 0, it is possible to state that: p(Q)+p(Q)q_j -c =0.

Applying the same method to firm i and considering that its output produced may be zero, we obtain:

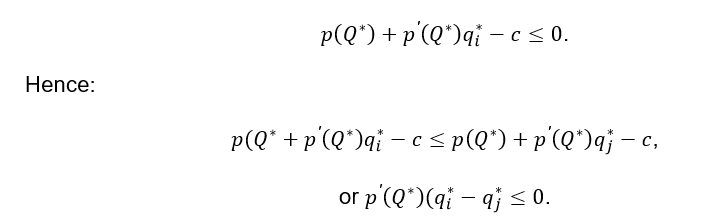
Since p(Q)<0, then q_j ≤ q^_i , which contradicts to the assumption that outputs of the firms are different in the equilibrium. Thus, the first assumption made was wrong and the output produced will be the same for each firm in the Cournot equilibrium:

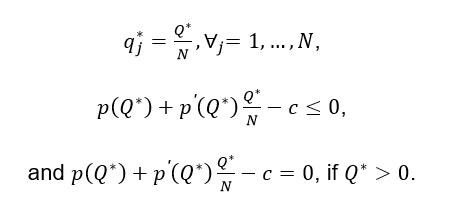
It should be mentioned that in the Cournot equilibrium, the output produced cannot be equal to zero, as if one puts Q=0 in the equation above, p(0) – c ≤ 0, which contradicts p(0)>c

Hence, the whole output in the Cournot equilibrium is described using the following equation: p(Q) + p(Q)xQ/N=c.

To conclude, the imposed tariff will not impact the output produced as long as new marginal costs are equal to marginal revenue; the outputs of companies are symmetrical.

Works Cited

Khoi, Luu Xuan, et al. “Oligopoly Model and Its Applications in International Trade.” Beyond Traditional Probabilistic Methods in Economics, edited by Vladik Kreinovich et al., Springer, 2019, pp. 296-310.

“Kinked demand.” Wikipedia: The Free Encyclopedia. Wikipedia Foundation, Inc. 2018. Web.

McAfee, Randolph Preston, et al. Introduction to Economic Analysis. Version 2.1, Creative Commons, 2008.