Assuming that a business productivity project was done for a company, it would be first presented to the consulting company for approval before sending it to the prospective client for review. This project focused on a business development initiative that established the stages, which a prospective business person or entity should consider when developing a better strategy for the success of the company (Schmidt, 2009). In addition, it was developed to provide a prospective client with a clear overview of the proposed project so that he or she could determine whether to proceed with the project (Schmidt, 2009).
Table 1: Durations for Each Activity.
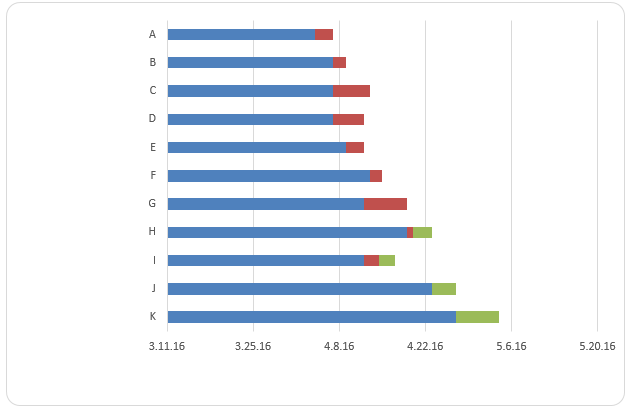
Project Timeline under Normal Circumstances
A Critical Path Analysis for the Network
Assuming that the project started on 4/3/12, crashing some tasks during the implementation did not change the length of time the, but only alter the time those activities took to end. For instance, crashing task C for 2 days only made it end on the same day with task B. This could not affect task D since B, C and D can run concurrently after Activity A is complete. However, crashing task G affected the end of activity J by reducing its termination.
Consequently, this affected the start and end of activity K, a situation that reduced the project duration by 4 days. Instead of the project ending on 05/02/2012, crashing of task G made it end on 04/28/2012. Therefore, crashing some project activities could only be done after carefully considering the impacts and benefits of such action. Only profitable actions could be exercised on the entire implementation of the project.
The Earliest Start Time = EST of previous activity + Duration of previous activity = 0+ 3 = 3
Earliest Finish Time (EFT) (A) = EFT at end of following activity – Duration of following activity = 5 – 3 = 3
Latest Start Time (LST) = LST of previous activity + Duration of previous activity (A) = 0 + 3 = 3
Latest Finish Time (LFT) Time (A) = LFT at end of following activity – Duration of following activity = 5 – 2 =3
Notably, the calculated values for EST, EFT, LST, and LFT are always equal. This indicates that there is minimal impact of changing the project timeframe on the quality of its outcome.
The Slack Time for Each Activity = Latest Start Time – Earliest Start Time
- A = 3 – 0 = 3
- B = 4 – 3 =1
- C = 4 – 3 = 1
- D = 4 – 3 = 1
- E = 6 – 5 = 1
- F = 10 – 2 = 8
- G = 9 – 8 = 1
- H = 16 – 3 = 13
- I = 19 – 1 = 18
- J = 20 – 21 = 1
- K = 24 – 23 = 1
Identify the Critical Path
In this project, the critical path is A C F G H J K. this path is considered critical because Activity C can only commence after A is complete, F comes after C, G starts after F, H begins after G, J starts after H, and K only commences after J is complete.
Assuming that the organization will receive a $1,000 bonus for each day the duration of the project is shortened. Secondly, the organization is also responsible for paying the crash cost associated with shortening the schedule. Therefore, to maximize the net profit, the task that should be crashed is G. This activity will be crashed by 4 days, meaning that the company will receive 4 x $1,000 = $4,000. Alternatively, the crash cost for this activity will be 4 x $600 = $2,400. The profit will be $4,000 – $2,400 = $1,600.
The project aims to make the implementing organisation improve the overall productivity. The main objectives of the project included various elements. First, it aimed to improve efficiency and effectiveness in the operations (Kerzner, 2009). Second, the project intended to improve the client’s productivity in terms of quantity and quality (Kerzner, 2009). Third, it sought to streamline the production operations and monitoring process to advice for necessary alterations in the production (Kerzner, 2009). This meant that the implementing company maximises on the use of its resources. This was necessary and significant for the project’s success.
References
Kerzner, H. (2009). Project Management: A Systems Approach to Planning, Scheduling, and Controlling. New York, NY: Wiley.
Schmidt, T. (2009). Strategic Project Management Made Simple: Practical Tools for Leaders and Teams. New York, NY: Wiley.