Changes in Entropy Under Adiabatic, Isothermal, and Isobaric Conditions

Abstract

The second law of thermodynamics relates entropy with time and proposes that the universe generally favors increasing entropy. The purpose of this experiment was to use various thermodynamic equations for entropy to determine the total entropy of a system when copper metal was immersed in liquid nitrogen in a dewar. The net entropy for the system was found to be 46.81 J/K. On the other hand, the calculated heat capacity for the copper metal was 12.837 K/Jmol^-1, whereas the theoretical value was 24.44 K/Jmol^-1. This large discrepancy was attributed to heat losses to the surroundings that were not captured during the experiment as well as any experimental errors in measurement. With an accurate system that minimizes heat losses to the environment, calorimetry can be used to find the entropy of different chemical reactions.

Introduction

The first law of thermodynamics states that energy cannot be created nor destroyed but is transformed from one state to another.¹ Conversely, the second law of thermodynamics proposes that the entropy often increases as time advances and that the universe tends to move towards increasing entropy, which is denoted by ΔS.¹ Entropy can be defined as a thermodynamic measure that expresses the unattainability of a system’s thermal energy to be transformed into mechanical work, which is usually construed as the extent of disarray or arbitrariness in the system.²

Several chemical processes and reactions have been shown to increase the entropy of a system. For example, when the physical state of a substance is changed from solid to liquid or from liquid to gas, the resultant entropy of the system increases.³

This increase is attributed to the dissemination of particles from each other with increasing distance between them. Dissolving a solid or a liquid in a solvent also increases the entropy of a system. As solids and liquid dissolve, their particles are allowed to dissociate and spread within the solution thus increasing the entropy.⁴ Chemical reactions where the total number of particles increase from the reactants to products are also associated with increased entropy. For instance, the dissociation of one molecule of dinitrogen tetroxide into two molecules leads to the formation of two molecules of nitrogen dioxide, signifying a total increase in the number of molecules and an increase in entropy.

Temperature increases are also associated with a corresponding rise in entropy. This rise is explained by the fact that temperature increases the kinetic energy of particles thus allowing them to vibrate, separate, and move more in a disorganized manner. Chemical compounds with weak intermolecular forces between their atoms or molecules also have higher entropies than those joined by strong covalent bonds. On the other hand, increasing the mass of a substance leads to an increase in entropy because more particles are made available.³

Furthermore, as a molecule becomes more complex, entropy increases. Complexity can be determined by an increase in the number of atoms, mass, or size of the atoms. This knowledge basis can be used to predict the overall entropy of a system by examining the nature of the chemical reactions involved in the entire process.

Entropy can be determined experimentally using calorimetry, which is the measurement of the amount of heat gained or lost during a chemical reaction. The formula DS=q/T can be used in the experimental determination of enthalpy where DS denotes a change in enthalpy, q represents heat changes, and T denotes time.⁵ The SI unit for entropy is Joules/Kelvin. Therefore, the temperature must be measured using the Kelvin scale where absolute zero is the lowest temperature that can be attained by any substance.⁶ At these temperatures, all movements of atoms stop leading to zero entropy. The research question in this work was can the entropy of a gas-liquid system be measured accurately under laboratory conditions?

The purpose of this experiment was to relate thermodynamic equations for entropy to its applications under adiabatic, isothermal, and isobaric conditions as well as to determine the total entropy for a system. Other objectives included using entropy to identify reversible and reversible processes and compare the experimental outcomes for entropy changes to theoretical results. It was hypothesized that calorimetry was an effective method of determining the entropy of a system.

Methods

Room temperature was measured to the nearest ± 0.1^oC as well as the mass of the metal to the nearest 0.01 g and recorded. The mass of a dewar, filled halfway with liquid nitrogen, was recorded as a function of time for 10 minutes by first determining the rate of nitrogen loss in the form of heat outflows. With the timer still on, additional changes made to the system were recorded using an automated system. The metal sample was immersed into the dewar ensuring that it touched the bottom of the dewar gently and that it was completely immersed in the liquid nitrogen. The dewar’s cap was replaced immediately. The immersion time was recorded. The liquid nitrogen boiled vigorously and stopped after a final surge of fast boiling.

t that point, the metal had attained the temperature of the liquid nitrogen. The mass and temperature of the system were recorded for an additional 10 minutes to determine the evaporation rate of liquid nitrogen in the dewar. The remaining liquid nitrogen was decanted into a storage dewar while trapping the metal in a net to permit it to warm to room temperature. The experimental procedure was repeated to collect two sets of data, which were used in various thermodynamic calculations.

Results

The data collected for the mass of the liquid nitrogen and metal over time was recorded and used to plot Figures 1 and 2 for the first and second trials respectively. The slopes, intercepts, and changes in mass before the addition of the metal and cessation of boiling were calculated and used to find the average changes of mass for the two runs. Additional calculations were done using the equations indicated in the lab manual. Details regarding these calculations are indicated in the appendices. The outcomes of these calculations are summarized in Table 1. The net enthalpy for the system was found to be 46.81J/K (Table 1). Since the net entropy change (dS_sys) was greater than 0, the entire process was irreversible. The experimental (calculated) heat capacity of copper metal was compared to the theoretical value and used to perform an error analysis whose outcome is indicated in Table 2.

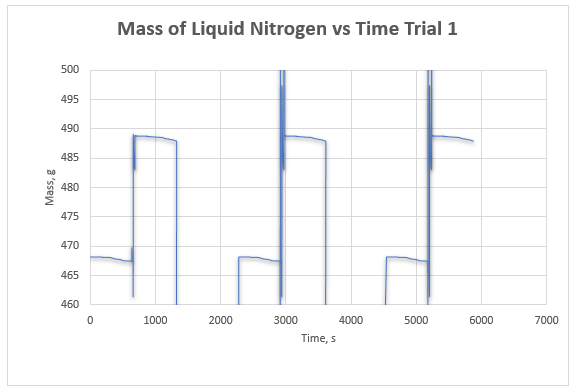
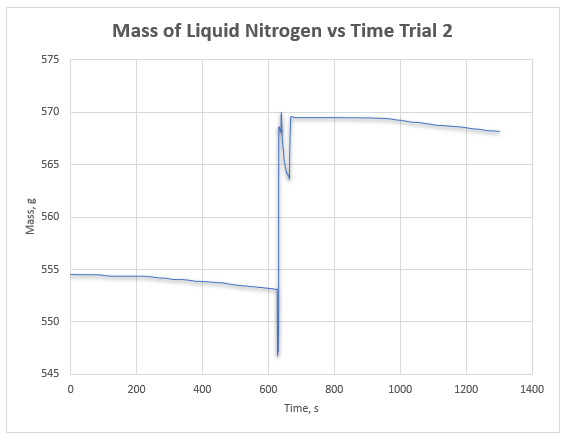
Table 1. A summary of entropy changes for different stages of the experiment, weight in grams and number of moles of N₂ lost to evaporation, and the heat capacity of copper metal.

Table 2. An error analysis of the calculated and published heat capacity of copper.

Discussion

Different activities throughout the entire experiment represented chemical modifications that were accompanied by entropy changes. The decrease in mass before the addition of the metal indicated the amount of nitrogen that was lost in the form of heat discharges. On the other hand, the net change in mass after immersing the copper metal was the amount of nitrogen that evaporated into the surroundings.

+The insertion of the metal into the dewar led to vigorous boiling of the liquid nitrogen, which led to the conversion of nitrogen from a liquid to a gas. This change led to an increase in the entropy of the system. The metal, which was at a higher temperature, introduced heat to the system following immersion. The heat was responsible for the evaporation of liquid nitrogen at its boiling point, which is a reversible process that normally takes place at constant pressure and temperature.³ In the experiment, this entropy change was given by ΔS₁, which was a negative value.

Conventionally, the entropy of vaporization is an increase in entropy when a liquid substance changes to vapor. This value is usually positive due to an increase in disorder as the liquid particles change to vapor. However, in this experiment, a negative value was recorded, which was against the norms. This observation could be attributed to unaccounted for heat losses or gains in the experiment. These experimental errors lead to what is known as enthalpy-entropy compensation.⁷

The cooling of the metal from room temperature to liquid nitrogen temperature was an isobaric process, which meant that the process occurred at constant pressure and that the resultant heat added to the system was used to alter the internal energy of the system.⁸ This entropy was denoted ΔS₂ and was found to be a negative value. Similarly, the warming of the nitrogen gas from liquid nitrogen temperature to room temperature was an isobaric process with an enthalpy change that was denoted by ΔS₃, which was a large positive value of 46.61 J/K. The heat capacity of the metal was determined by finding the sum of the enthalpy change for the cooling of the metal and the evaporation of the liquid nitrogen. Since the process was carried out adiabatically in a dewar, there was no heat transfer in and out of the system.

The heat input from the surroundings to the nitrogen gas was equal in magnitude but opposite in sign to the heat absorbed by the nitrogen gas. Therefore, entropy change in the surroundings remained constant and was given by ΔS₄ in the form of a slightly negative value of -0.167 J/K. The net entropy change for the system and its surroundings was found by adding the entropies of the individual steps, which was equal to 46.81 J/K. Since dS_sys yielded a value that was larger than 0, the entire process was irreversible. This conclusion was based on the assumptions of the second law of thermodynamics, which suggests that the total entropy of a system and its surroundings remain unchanged in a reversible reaction but increases in an irreversible reaction.⁹

The calculated heat capacity of copper metal was 12.837 K/Jmol^-1, whereas the theoretical heat capacity was 24.44 K/Jmol^-1.¹⁰ This difference gave a percentage error of 47.5%, which is a very big error that could be accounted for by several factors. For example, there were likely heat losses to the environment and the surroundings that were unaccounted for during the experiment. Other sources of errors include inaccuracies in the measurement of the mass of the copper metal or the overall sensitivity of the automated system that was used in measuring the temperature changes over time.

Conclusions

The purpose of the experiment was to use different thermodynamic equations to calculate the entropies under adiabatic, isothermal, and isobaric conditions. The overall entropy of the system when copper metal was immersed in a dewar containing liquid nitrogen was 46.81 J/K, which showed that the reaction was irreversible. The experimental heat capacity for the copper metal was found to be 12.837 K/Jmol^-1, which was 47.5% less than the theoretical value. This large error was attributed to unexplained heat losses to the surroundings. Overall, it was concluded that calorimetry was a reliable method of determining the entropy of a system. However, its accuracy was dependent on minimizing experimental errors.

Appendices

Before the addition of the metal, slope = -0.0013683, intercept = 468.3019.

Change of mass (m₁) = (657 x (-0.0013683) + 46803019) – (1 x (-0.0013683) + 468.3019) = -0.89763.

After cessation of boiling, slope = -0.001311921 489.8273

Change of mass (m₂) = (1333 x (-0.001312) + 489.8273) – (701 x (-0.001312) + 489.8273) = -0.82913.

The following data were obtained for the second trial.

Before the addition of the metal, slope = -0.0025303, intercept = 554.80881

Change of mass (m₁) = (630 x (-0.0025303) + 554.80881) – (1 x (-0.0025303) + 554.80881) = -1.57427.

After cessation of boiling, slope = -0.001981573, intercept = 571.0372531.

Change of mass (m₂) = (1302 x (-0.001981573) + 571.0372531) – (679 x (-0.001981573) +571.0372531) = -1.23452

The average changes of mass for the two runs was:

Before the addition of the metal (m₁) =-1.57427 – 0.89763/2= -1.236 g

After cessation of boiling (m₂) = – 1.23452 – 0.82913/2 = -1.0318 g

Molar enthalpy of vaporization of Liquid nitrogen is 6100 J/mol at 78K¹

Mass of nitrogen of that boiled off = (m₂-m₁) = (-1.0318 +1.236) = 0.2042 g

Moles of Nitrogen that boiled off = 0.2042g/28gx1 mole = 0.00729 moles

Entropy of evaporation (ΔS1)

=0.00729molx6100Jmol/78K = 0.57012 J/K

Enthalpy change in cooling of the metal from room temperature to the liquid nitrogen

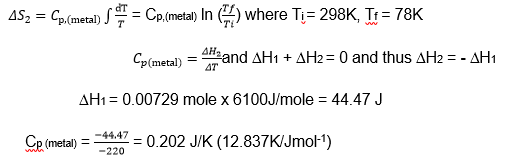
ΔS2 = 0.202 ln) = -0.2707 J/K; ΔS3

The entropy change for warming of the nitrogen gas from liquid nitrogen temperature to room temperature is given by

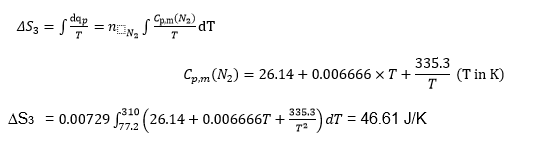
Entropy change of the surroundings =

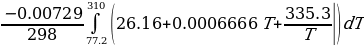ΔS4 =  = -0.167 J/K

Net entropy = ΔS₁ + ΔS₂ + ΔS₃ + ΔS₄ = 0.5701 + (-0.2707) + (46.61) + (-0.167) = 46.81J/K

Entropy change of the metal = n_cu 

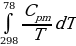
Average mass of copper = 38.648+31.6679/2 = 35.1579 g

Moles of copper =35.1579/63.55×1 mole=0.5532mol

Entropy Change = 0.5532 x (-0.202) ln (78/298 = 0.149J/Kmol^-1

Since dS_sys  0. The entire process is irreversible.

References

Seifert, U. First and Second Law of Thermodynamics at Strong Coupling. Phys. Rev. Lett. 2016, 116, 1-5.

Flores-Gallegos, N. A New Approach of Shannon’s Entropy in Atoms. Chem. Phys. Lett. 2016, 650, 57-59.

Chan, K.S.; Tan, J. Understanding Advanced Physical Inorganic Chemistry: The Learner’s Approach; World Scientific: Singapore, 2016.

Toh, C.S. A-Level Study Guide Chemistry Ed H2.2; Step-by-Step International: Singapore, 2016.

Evans, D.J.; Searles, D.J.; Williams, S.R. A Derivation of the Gibbs Equation and the Determination of Change in Gibbs Entropy from Calorimetry. Aust. J. Chem. 2017, 69, 1413-1419.

Mahto, D.; Singh, A.K.; Kumari, N. Change in Internal Energy and Enthalpy of Spinning Black Hole with Half Spin Parameter in XRBs. IJAA. 2016, 6, 328-333.

Perez-Benito, J.F.; Mulero-Raichs, M. Enthalpy–Entropy Compensation Effect in Chemical Kinetics and Experimental Errors: A Numerical Simulation Approach. J. Phys. Chem. A. 2016, 120, 7598-7609.

Stouffs, P. Comment on “Energy and Entropy Analysis of Closed Adiabatic Expansion Based Trilateral Cycles” By Ramon Ferreiro Garcia, Jose Carbia Carril, Javier Romero Gomez, Manuel Romero Gomez [Energy Convers. Manage. 119 (2016) 49–59]. Energy Convers. Manag. 2016, 123, 643-645.

Chen, L.; Zhang, L.; Xia, S.; Sun, F. Entropy Generation Minimization for CO₂ Hydrogenation to Light Olefins. Energy. 2018, 147, 187-196.

NIST Chemistry WebBook, SRD 69. Web.