Introduction
This report was commissioned by the CEO of D. M. Pan National Real Estate. The purpose of this report is to provide a benchmark price for square foot of real estate based on the statistical analysis of the real estate prices in the US in 2019. The central question this report aims at answering is, ‘what benchmark price should D. M. Pan National Real Estate to list houses based on square footage. In order to answer this question, the report uses a dataset of 50 randomly selected houses in different parts of the US to create a linear regression model that would provide an equation for pricing the houses.
Creating a linear regression model is most appropriate when there is a strong correlation between a predictor and an outcome variable. A scatterplot for such a relationship looks a collection of dots scattered around a straight line that is either ascending or descending. A predictor variable is an independent variable that affects the response variable if manipulated. A response variable is dependent to some extent on the predictor variable. Since the square footage is assumed to affect the price of the real estate positively, the price was selected to be a response variable and the square footage was selected to be a predictor variable.
Data Collection
The data for the analysis was collected from a dataset of 1,000 entries that included prices, square footage, and prices per square foot of real estate objects all over the US with their location in terms region, state, and county. A random sample of 50 entries was selected using Microsoft Excel by creating a new column with a random number, sorting the list of entries according to the random number, and selecting first 50 entries. The predictor variable (x-axis) was square footage of the house, while the responses variable (y-axis) was the price of the house. The data is visualized in Figure 1 below using a scatterplot.
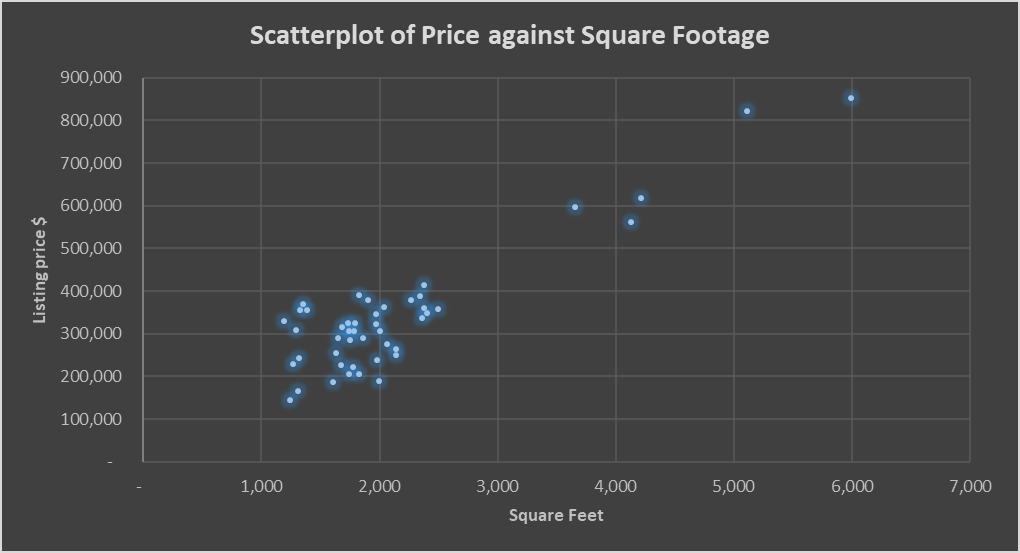
The scatterplot demonstrates that the dots on the graph are clustered along an ascending straight line, which is a sign of a linear correlation. Thus, using a linear regression model for predicting the listing price is appropriate.
Data Analysis
Before conducting regression analysis, descriptive analysis of the variables was conducting using summary statistics and histograms. The histograms for square footage and listing price of the sample are provided in Figures 2 and 3 correspondingly. Summary statistics of the sample are provided in Table 1 below.
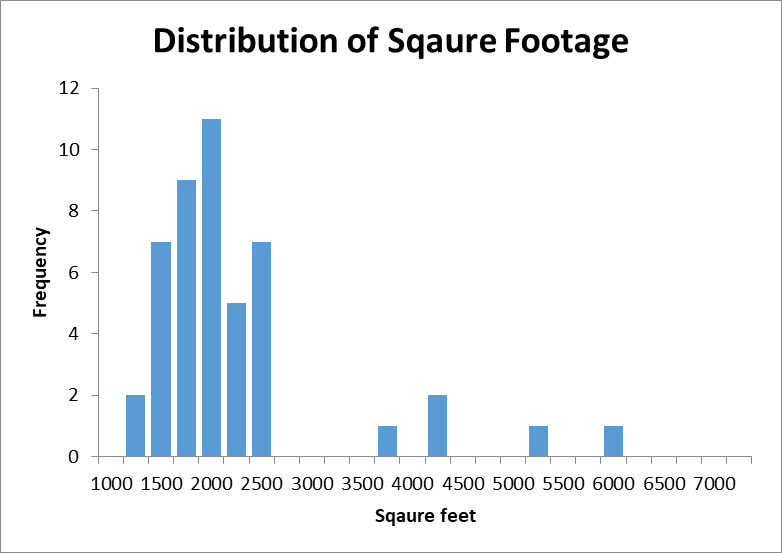
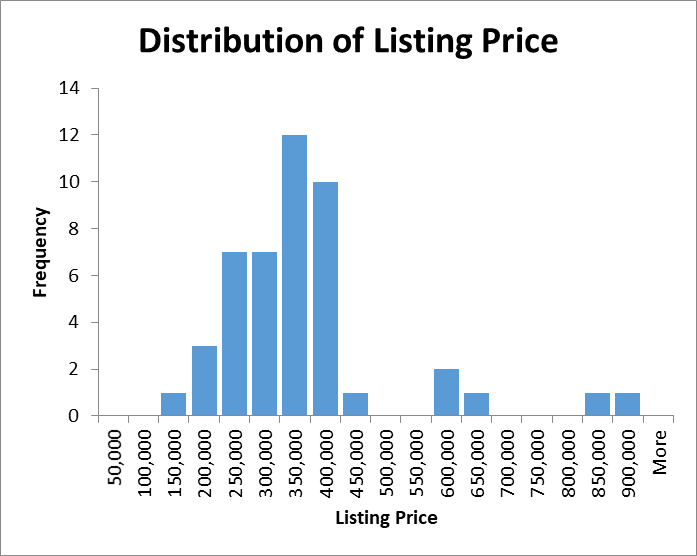
Table 1. Descriptive sample statistics
The analysis demonstrates that the distribution of the square footage wand the listing prices were close to normal with a positive skew, as the values were clustered on the left side of the distribution. The distributions also appear to be highly leptokurtic, as they are concentrated around the mean. There are also significant gaps and outliers on the right side of the distributions. The presence of outliers may have affected them mean value. The average square footage of the houses was 2,122 with a standard deviation of 985 and a median value of 1,843. The average listing price was $339,450 with a standard deviation of 145,568 and a median of $319,900. Since the distribution were affected by extreme outliers, it is best to use the medians as measures of central tendency.
The sample is representative of the population, as the descriptive statistics and the histograms of the population were close to the sample descriptives and distribution. The histograms for square footage and listing price of the population are provided in Figures 4 and 5 correspondingly. Summary statistics of the population are provided in Table 2 below.
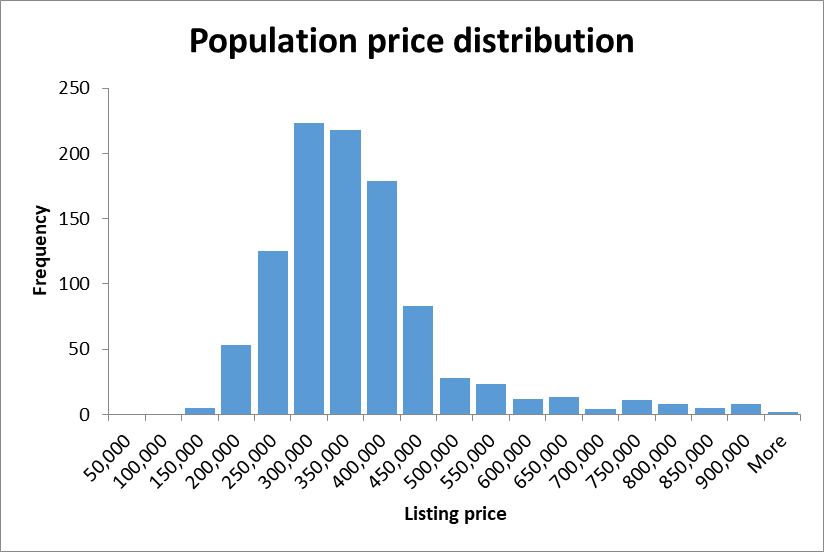
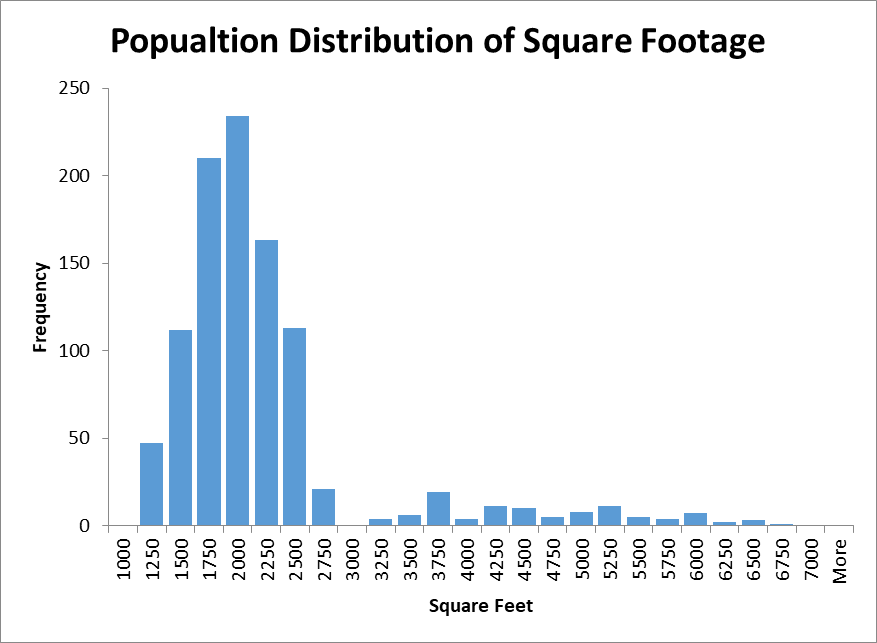
Table 1. Descriptive sample statistics
The Regression Model
A scatterplot with a trendline was created to assess if a regression model could be created. The scatterplot is provided int Figure 6 below. The analysis of the scatterplot revealed that a regression model could be created, as the values were scatter around the trendline.
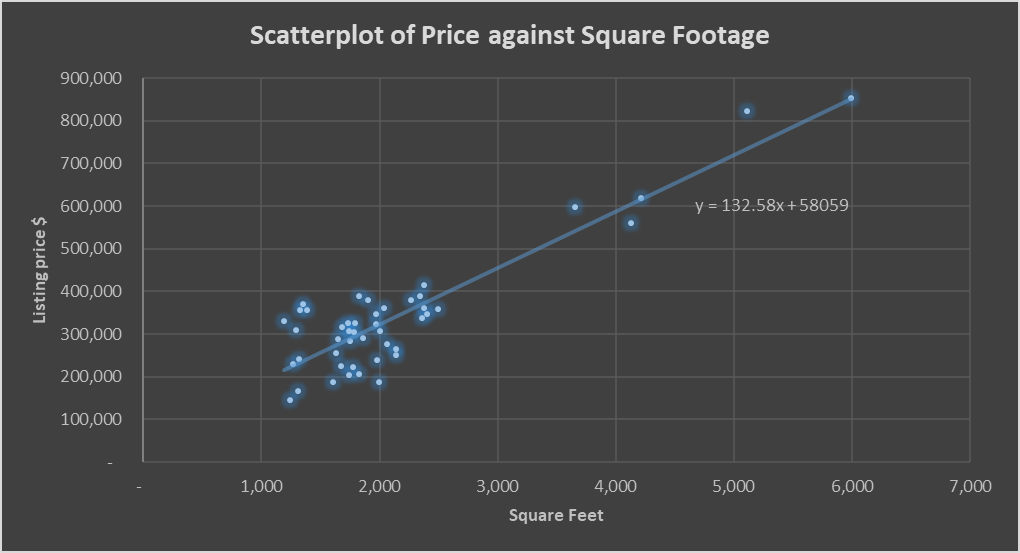
The analysis of the model demonstrated that the relationship between the variables is positive, as the trendline is ascending. This implies that that higher the square footage of the house, the higher the listing price. The effect of the square footage of the house is strong, as the line was steep with almost 45 degrees angle. Even though the model had some outliers, it is best to keep them, as they capture important information for the larger-than-usual houses. Peason’s correlation coefficient (Pearson’s r) was 0.9, which confirms that the correlation between the variables was very strong.
The Line of Best Fit
Regression analysis demonstrated that the listing price could be predicted using the following equasion:
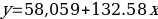
Where y is the listing price, and x is the square footage of a house.
The regression model demonstrates that an increase in the area of the house by one square foot increases the listing price by $132.58. The listing price also appears to have a constant of $58,059 which is added to the variable part of the listing price. The coefficient of determination was R2 = 0.805, which means that the 80.5% of changes in the listing price can be explained by the changes in the square footage of the house.
My house is 1,950 square feet. Thus, considering the regression equation the listing price should be:
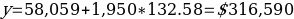
Conclusions
The results of the analysis demonstrated that the area of the house highly affects the listing price, as it was expected. The created equation for predicting the listing price was found to be useful for creating the benchmark price of the house listings. However, since the model explains only 80% of changes, consideration of additional variables, like state, county, or region may lead to different results. Thus, future research should focus on adding location variables to analysis to calculate a more accurate benchmark price.