In the paper, the returns and quarterly earnings of Apple Inc. will be analyzed. The company is a component of the S&P 500 index. The analysis will be carried out for a period of 5 years.
Returns
The share prices for a day before and a day after the announcement of quarterly results are collected. Further, the percentage change of these values is calculated to estimate the impact of the announcement.
There is a tendency to share prices to improve after the announcement of quarterly results if the results met expectations. However, the share prices are affected by several factors and not only the announcement of results.
Earnings
The company reported higher earnings in the first quarter, and the earnings dropped as the year progresses.
Descriptive statistics
The average of the earnings was 8.0625, while the standard deviation was 3.0842. The highest value of earnings during the entire period was $13.6b, while the least value was $3.07b.
Regression
The regression model will build a linear relationship between the time period and earnings. The regression line will take the form;
- Y = a + bX
Y represents the earnings, while X represents the time period. The results of the regression are presented below.
The regression will take the form Y = 4.9192 + 0.2993X. The value of R-square (0.3297) shows that the regression line is weak. The estimated earnings for next quarter is $11.21 billion (Y = 4.9192 + 0.2993 * 21).
Test of significance
A two-tailed t-test will be used to test the significance of the explanatory variable.
- Null hypothesis: Ho: Xi = 0
- Alternative hypothesis: Ho: Xi ≠ 0
The null hypothesis implies that the variable is not a significant determinant of movements in stock prices. The t-statistic for the time period is 2.975755, while the p-value is 0.008101. Since the p-value is less than α = 0.05, the null hypothesis is rejected. This implies that the time period is a significant determinant of earnings (Evans, 2014).
F – test
The overall significance of the regression model can be analyzed using an F – test at the 5% significance level.
Null hypothesis H0: β0 = β1
Alternative hypothesis H1: βj ≠ 0, for at least one value of j
The null hypothesis implies that the overall regression line is not significant. From the regression results, the value of f-calculated is 8.8551, while the p-value is 0.008101. The p-value is less than α = 0.05. This shows that the overall regression line is significant (Evans, 2014).
Control limits
Mean earnings
= total earnings / total number of days
= 161.25 / 20
= 8.0625
The upper and lower control limit will be calculated using the formula presented below.

The graph presented below shows the control chart.
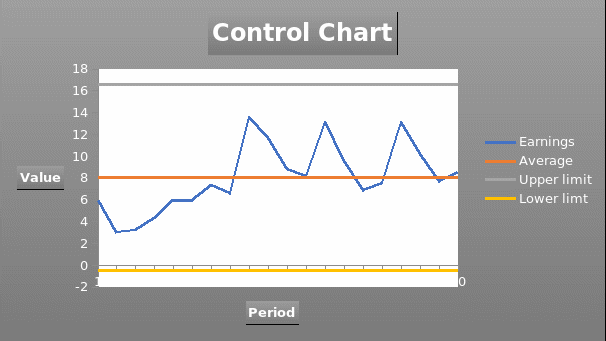
The graph shows that the process is in control because the quarterly earnings are within the upper and control limit.
3 period moving average
Thus, the estimated earnings for the next quarter is $10.33 billion.
Reference
Evans, J. (2014). Business analytics: methods, methods, and decisions. USA: Pearson Education Limited. Web.