Introduction
This paper provides a discussion on description and analysis of data. For this population, the population statistics of UK for the years from 1970 to 2006 has been used. Data was obtained from the World Bank site (WB. 2008).
Description of Data accessing
The data selected for the paper is the growth in population of United Kingdom for the years from 1970 to 2007. Studies of population growth or decrease are very important in understanding the economic growth of a country. If the population has increased then it means that the economic indicators like GDP and revenue has to improve to feed the increase in the population. World bank maintains detailed data of many countries and data on key economic indicators is provided for researchers and students, free of cost. I accessed the home page of the World Bank and ran a query with filters so that only data related to population growth was obtained.
The world Bank database is very powerful and allowed me to select multiple countries, one or more variables and also select the year range. The data base has details from 1960 to 2006 and I could select the required range of years. It is also possible to select different years randomly. After the variable were selected, I had to click the show report button and all the data were displayed on the screen. The database also allowed the data to be exported to an xls file and I saved the xls file to my hard disk for later reference. Please refer to Appendix for the detailed data.
Descriptive Statistics
I used the Descriptive Statistics command in MS Excel for the population range and the results are shown in the following table.
Table 1. Descriptive Statistical Analysis.
A brief description of the terms are given as below (Hoffman, 2003):
- Mean: The mean is the average of the scores in the population. Numerically, it equals the sum of the scores divided by the number of scores. It is of interest that the mean is the one value which, if substituted for every score in a population, would yield the same sum as the original scores, and hence it would yield the same mean. The mean for the data is 57531219.12.
- Standard Error: The Standard Error is an estimate of the standard deviation of the sampling distribution of means, based on the data from one or more random samples. Numerically, it is equal to the square root of the quantity obtained when s squared is divided by the size of the sample. Standard error for this data is 232385.52.
- Median The median is one of several indices of central tendency that statisticians use to indicate the point on the scale of measures where the population is centred. The median of a population is the point that divides the distribution of scores in half. Numerically, half of the scores in a population will have values that are equal to or larger than the median and half will have values that are equal to or smaller than the median. Median for this data is 57158000.
- Standard Deviation: The standard deviation is one of several indices of variability that statisticians use to characterize the dispersion among the measures in a given population. To calculate the standard deviation of a population it is first necessary to calculate that population’s variance. Numerically, the standard deviation is the square root of the variance. Unlike the variance, which is a somewhat abstract measure of variability, the standard deviation can be readily conceptualised as a distance along the scale of measurement. Standard deviation for this data is 1413545.937.
- Kurtosis: Kurtosis is a measure of whether the data are peaked or flat relative to a normal distribution. The value of Kurtosis is -0.881085627 meaning that the data is skewed to the left side.
- Skewness: This is a parameter that describes asymmetry in a random variable’s probability distribution. The value for skewness is 0.606235903.
- Range: The range is the distance between the highest and lowest score. Numerically, the range equals the highest score minus the lowest score. The value for Range is 4918100.
- Minimum/ Smallest: This is the smallest value in the data range and represents the smallest value. The minimum value is 55632000.
- Maximum/ Largest: This is the largest value in the data range and represents the largest value. The maximum value is 60550100.
- Sum: This is the summation of all the values in the data range. The value in this data range is 2128655108.
- Count: This is the total number of rows or individual data that the dataset has. Since the example taken is small, it is possible to count the number of row and it is 37. But when thousands of data are studied then it is not possible to count the values.
Histogram
A histogram is a way of graphically showing the characteristics of the distribution of items in a given population or sample. In a histogram each measure is represented by a single block that is placed over the midpoint of the class interval into which the measure falls. The histogram for the dataset is shown in the following table.
Table 2. Histogram.
A chart of the histogram plot is as shown below.
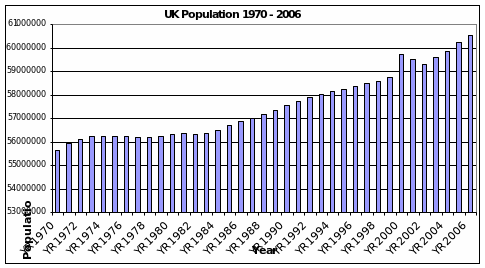
As seen in the above chart, the population rise has been low for the years up to 1984. From then on, the rise has risen more and there was a brief spike in 2000 followed by a fall for the next two years. Again the population is rising from 2004 onwards. The graph gives a clear idea of how the population is rising and following for the years from 1970 t0 2006.
Confidence Interval and Unknown Population Parameter
Confidence interval gives an estimated range of values, which is likely to include an unknown population parameter, the estimated range being calculated from a given set of sample data. If independent samples are taken repeatedly from the same population, and a confidence interval calculated for each sample, then a certain percentage (confidence level) of the intervals will include the unknown population parameter. Confidence intervals are usually calculated so that this percentage is 95%, but we can produce 90%, 99%, 99.9% (or whatever) confidence intervals for the unknown parameter. The width of the confidence interval gives us some idea about how uncertain we are about the unknown parameter. A very wide interval may indicate that more data should be collected before anything very definite can be said about the parameter.
The confidence interval has been obtained using the Excel function and at 95%, the value for the unknown population parameter is 471299.0597.
References
Hoffman Russell D. 2003. Glossary of Statistics terms. Web.
WB. 2008. United Kingdom, Population Statistics. Web.
Appendix
Table of UK population data from 1970 to 2006 (WB, 2008).